Lode's Computer Graphics Tutorial

Julia and Mandelbrot Sets

Table of Contents

Back to Index

Introduction

The Julia Set and Mandelbrot Set are those quite well known sets on the complex plane that create those pretty infinitely detailed images. They're so pretty, that there is even art created with them. The Mandelbrot Set isn't a real fractals by definition, but it's semi self similar and still shows infinite detail, so it's usually called a fractal as well.

Research on Julia Sets was done in 1917 by Gaston Julia himself, but he didn't have a computer available to actually draw it. The topic didn't gain much interest, until in the 1970s, Benout Mandelbrot drew Julia Sets on a computer, and discovered the Mandelbrot set.

This tutorial will only cover the basics of the theory (there's much more to tell about the Julia and Mandelbrot sets), and the code to draw them. Apart from that, more code is included of some pretty handy fractal viewers where you can zoom and move around on the fly.

Julia Set

This chapter first tries to explain a bit of the mathematical formulas behind Julia Sets, more specifically, Quadratic Julia Sets. Knowledge about complex numbers is required, so if you need it you can read the appendix about complex numbers.

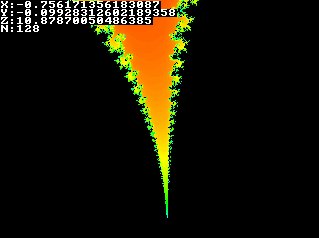
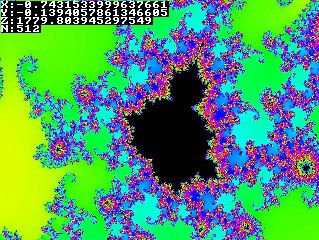
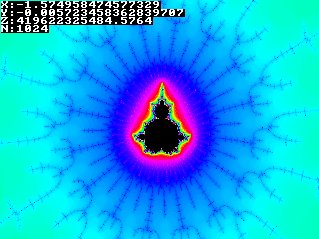
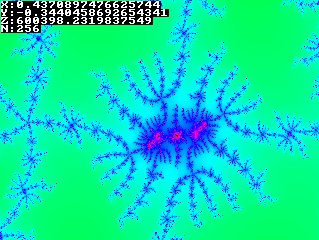
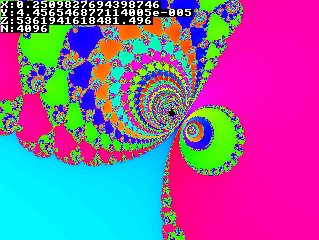
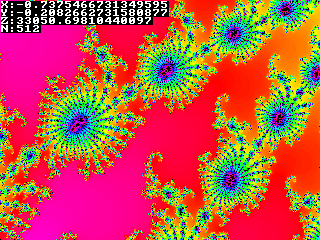
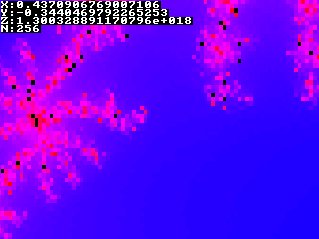
So how to generate such a beautiful fractal? In short: for every pixel, iterate znew = zold² + c on the complex plane until it leaves the circle around the origin with radius 2. The number of iterations it the color of the pixel.

The screen will be representing a part of the complex plane, inside the circle with radius 2 around the origin. For a pixel, the x coordinate will represent the real part of its complex coordinates, and the y coordinate will be the imaginary part.

For a julia set, for each pixel apply an iterated complex function. This function is newz = oldz² + c, with z and c both being complex numbers. Z is initially the coordinates of the pixel, and will then constantly be updated through every iteration: each iteration, the "newz" of the previous iteration is now used as "oldz".

If you keep iterating this function, depending on the initial condition (the pixel), z will either go to infinity, or remain in the circle with radius 2 around the origin of the complex plane forever. The points that remain in the circle forever, are the ones that belong to the Julia Set. So keep iterating the function until the distance of z to the origin (0,0) is greater than 2. Also give a maximum number of iterations, for example 256, or the computer would be stuck in an endless loop.

The color value of the pixel will then become the number of times we had to iterate the function before the distance of z to the origin got larger than 2. The constant c in the formula can be anything really, as long as it's also inside the circle with radius 2. Different values of c give different Julia Sets. Some Julia Sets are connected, others aren't. The Mandelbrot Set is the collection of all  points c that generate a connected Julia Set.

Here's an example of the calculations:

First, you can choose a constant c for the function, which one you choose will determinate the shape of the fractal. Let's take c = (-0.5,0.5) in this example, so -0.5 is the real part and 0.5 the imaginary part.

Imagine we're currently calculating the color of pixel (256,192) on a 256*256 screen. First, we transform the coordinates so it lies between -1 and 1 (if you zoom or move around in the fractal a different transformation is required): the coordinates become (1,0.5) so p = 1 + 0.5i.

Now we apply the function for the first time:

z = p² + c
  = (1 + 0.5i)² - 0.5 + 0.5i
  = 1 + 2*0.5i + 0.25*i² - 0.5 + 0.5i
  = 0.5 + 1.5i - 0.25
  = 0.25 + 1.5i

So z = (0.25,1.5), and the distance of z to the origin = sqrt(0.25*0.25 + 1.5*1.5) = 1.52069... is still smaller than 2.

Now you take this calculated z and put it in the function again to calculate the next z, so now we get

z = (0.25 + 1.5i)² - 0.5 + 0.5i
  = 0.0625 + 2*0.375i - 2.25 - 0.5 + 0.5i
  = -2.6875 + 1.25i

The distance is now 8.78515625, so we're outside the circle with radius 2, and we now know the point is outside the julia set. The number of iterations was now only 2, so the pixel gets color value 2 and we're done.  Some start values give more than 256 iterations, and depending on how much maximal iterations you've set, you can then stop or keep continuing.

The more iterations, the more detailed the Julia set will look when zooming in deeply, but the more calculations are needed. The higher the precision of the numbers, the longer you can zoom in without encountering blocky pixels.

Here's the source code of a program that'll draw a Julia Set. Put this in the main.cpp file, inside the "int main(int argc, char *argv[])" function. The comments in it are made blue and explain most of the code. The code doesn't use complex numbers but normal floating point numbers, the real and imaginary part are simply calculated separately, like you'd do by hand.

int main(int argc, char *argv[])
{
  screen(400, 300, 0, "Julia Set"); //make larger to see more detail!

  //each iteration, it calculates: new = old*old + c, where c is a constant and old starts at current pixel
  double cRe, cIm;           //real and imaginary part of the constant c, determinate shape of the Julia Set
  double newRe, newIm, oldRe, oldIm;   //real and imaginary parts of new and old
  double zoom = 1, moveX = 0, moveY = 0; //you can change these to zoom and change position
  ColorRGB color; //the RGB color value for the pixel
  int maxIterations = 300; //after how much iterations the function should stop

  //pick some values for the constant c, this determines the shape of the Julia Set
  cRe = -0.7;
  cIm = 0.27015;

  //loop through every pixel
  for(int y = 0; y < h; y++)
  for(int x = 0; x < w; x++)
  {
    //calculate the initial real and imaginary part of z, based on the pixel location and zoom and position values
    newRe = 1.5 * (x - w / 2) / (0.5 * zoom * w) + moveX;
    newIm = (y - h / 2) / (0.5 * zoom * h) + moveY;
    //i will represent the number of iterations
    int i;
    //start the iteration process
    for(i = 0; i < maxIterations; i++)
    {
      //remember value of previous iteration
      oldRe = newRe;
      oldIm = newIm;
      //the actual iteration, the real and imaginary part are calculated
      newRe = oldRe * oldRe - oldIm * oldIm + cRe;
      newIm = 2 * oldRe * oldIm + cIm;
      //if the point is outside the circle with radius 2: stop
      if((newRe * newRe + newIm * newIm) > 4) break;
    }
    //use color model conversion to get rainbow palette, make brightness black if maxIterations reached
    color = HSVtoRGB(ColorHSV(i % 256, 255, 255 * (i < maxIterations)));
    //draw the pixel
    pset(x, y, color);
  }
  //make the Julia Set visible and wait to exit
  redraw();
  sleep();
  return 0;
}

The parameter of the number of iterations is used for the "Hue" of the HSV color model. The advantage of Hue is that it's circular, so no matter how many maximum iterations there are, the Hue based color palette will always keep generating nice continuous values.

The result looks like this:


Julia Explorer

You can change the values "zoom", "moveX" and "moveY" in the above code to zoom in at certain positions, but much better would be if you could do this in realtime while the program is running, for example by pressing the arrow keys to move, and the keypad + and - keys to zoom in/out. Even better would be if you could use the keypad arrow keys to change the values of cRe and cIm to change the shape of the Julia Set in realtime.

Programming something that can do that is pretty simple, just use the SDL keys to change the values of those variables and draw the Julia Set every time again in a loop! The following code does all that and  also shows the values of all those variables on screen, so that you know exactly at what coordinates of the Julia Set the nice things are. It'll also let you change the value "maxIterations" etc... The comments in the code should explain it all again. There isn't any new computer graphics code, just input keys that change parameters:

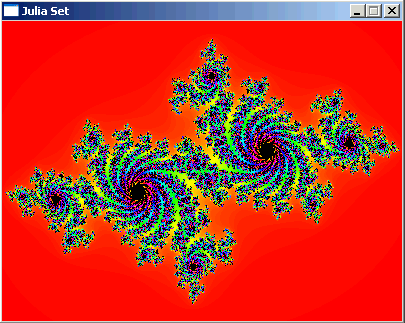
int main(int argc, char *argv[])
{
  screen(320, 240, 0, "Julia  Explorer");

  //each iteration, it calculates: new = old*old + c, where c is a constant and old starts at current pixel
  double cRe, cIm;           //real and imaginary part of the constant c, determines shape of the Julia Set
  double newRe, newIm, oldRe, oldIm;   //real and imaginary parts of new and old
  double zoom=1, moveX=0, moveY=0; //you can change these to zoom and change position
  ColorRGB color; //the RGB color value for the pixel
  int maxIterations=128; //after how much iterations the function should stop

  double time, oldTime, frameTime; //current and old time, and their difference (for input)
  int showText=0;

  //pick some values for the constant c, this determines the shape of the Julia Set
  cRe = -0.7;
  cIm = 0.27015;

  //begin the program loop
  while(!done())
  {
    //draw the fractal
    for(int y = 0; y < h; y++)
    for(int x = 0; x < w; x++)
    {
      //calculate the initial real and imaginary part of z, based on the pixel location and zoom and position values
      newRe = 1.5 * (x - w / 2) / (0.5 * zoom * w) + moveX;
      newIm = (y - h / 2) / (0.5 * zoom * h) + moveY;
      //i will represent the number of iterations
      int i;
      //start the iteration process
      for(i = 0; i < maxIterations; i++)
      {
        //remember value of previous iteration
        oldRe = newRe;
        oldIm = newIm;
        //the actual iteration, the real and imaginary part are calculated
        newRe = oldRe * oldRe - oldIm * oldIm + cRe;
        newIm = 2 * oldRe * oldIm + cIm;
        //if the point is outside the circle with radius 2: stop
        if((newRe * newRe + newIm * newIm) > 4) break;
      }
      //use color model conversion to get rainbow palette, make brightness black if maxIterations reached
      color = HSVtoRGB(ColorHSV(i % 256, 255, 255 * (i < maxIterations)));
      //draw the pixel
      pset(x, y, color);
    }

    //print the values of all variables on screen if that option is enabled
    if(showText <= 1)
    {
      print("X:", 1, 1, RGB_White, 1); print(moveX, 17, 1, RGB_White, 1);
      print("Y:", 1, 9, RGB_White, 1); print(moveY, 17, 9, RGB_White, 1);
      print("Z:", 1, 17, RGB_White, 1); print(zoom, 17, 17, RGB_White, 1);
      print("R:", 1, 25, RGB_White, 1); print(cRe, 17, 25, RGB_White, 1);
      print("I:", 1, 33, RGB_White, 1); print(cIm, 17, 33, RGB_White, 1);
      print("N:", 1, 41, RGB_White, 1); print(maxIterations, 17, 41, RGB_White, 1);
    }
    //print the help text on screen if that option is enabled
    if(showText == 0)
    {
      print("Arrows move (X,Y), Keypad +,- zooms (Z)", 1, h - 33, RGB_White, 1);
      print("Keypad arrows change shape (R,I)     ", 1, h - 25, RGB_White, 1);
      print("Keypad *,/ changes iterations (N)    ", 1, h - 17, RGB_White, 1);
      print("a to z=presets (qwerty), F1=cycle texts", 1, h - 9, RGB_White, 1);
    }
    redraw();

    //get the time and old time for time dependent input
    oldTime = time;
    time = getTicks();
    frameTime = time - oldTime;
    readKeys();
    //ZOOM keys
    if(keyDown(SDLK_KP_PLUS))  {zoom *= pow(1.001, frameTime);}
    if(keyDown(SDLK_KP_MINUS)) {zoom /= pow(1.001, frameTime);}
    //MOVE keys
    if(keyDown(SDLK_DOWN))  {moveY += 0.0003 * frameTime / zoom;}
    if(keyDown(SDLK_UP))  {moveY -= 0.0003 * frameTime / zoom;}
    if(keyDown(SDLK_RIGHT)) {moveX += 0.0003 * frameTime / zoom;}
    if(keyDown(SDLK_LEFT))  {moveX -= 0.0003 * frameTime / zoom;}
    //CHANGE SHAPE keys
    if(keyDown(SDLK_KP2)) {cIm += 0.0002 * frameTime / zoom;}
    if(keyDown(SDLK_KP8)) {cIm -= 0.0002 * frameTime / zoom;}
    if(keyDown(SDLK_KP6)) {cRe += 0.0002 * frameTime / zoom;}
    if(keyDown(SDLK_KP4)) {cRe -= 0.0002 * frameTime / zoom;}
    //keys to change number of iterations
    if(keyPressed(SDLK_KP_MULTIPLY)) {maxIterations *= 2;}
    if(keyPressed(SDLK_KP_DIVIDE))   {if(maxIterations > 2) maxIterations /= 2;}
    //key to change the text options
    if(keyPressed(SDLK_F1)) {showText++; showText %= 3;}
  }
}

Now you can explore all the details of every possible Julia Set! Find a nice shape with the keypad numbers, then move with the arrow keys to a border or interesting spot of the julia set, and start zooming in to see more detail. If you've zoomed in, you may want to press the numpad "*" button to see more detail.

Note: in the current version of gcc, the pow function doesn't work if you mix floats and doubles, so make sure either everything is double, or everything is float.

Here are some screenshots:

A few different shapes:


Zooming in:


Increasing the number of iterations:


Mandelbrot Set

When zooming in, you'll keep seeing the same details over and over in a Julia Set - it's a fractal after all. The Mandelbrot set isn't completely self similar, it's only semi self similar, so in a Mandelbrot set much more surprises can turn up when zooming in.

The mandelbrot set represents every complex point c for which the Julia Set will be connected, or every Julia Set that contains the origin. To generate a mandelbrot set you use the same iterative function as the Julia Set, only this time c will represent the position of the pixel, and z will start at (0,0)

The following code is very similar to the Julia Set drawer, only it'll output a Mandelbrot Set with rainbow palette instead. The changed parts are indicated in bold.

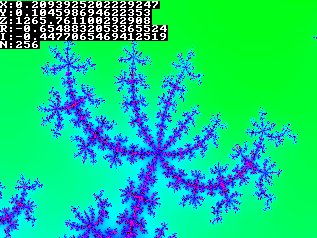
int main(int argc, char *argv[])
{
  screen(400, 300, 0, "Mandelbrot Set"); //make larger to see more detail!

  //each iteration, it calculates: newz = oldz*oldz + p, where p is the current pixel, and oldz stars at the origin
  double pr, pi;           //real and imaginary part of the pixel p
  double newRe, newIm, oldRe, oldIm;   //real and imaginary parts of new and old z
  double zoom = 1, moveX = -0.5, moveY = 0; //you can change these to zoom and change position
  ColorRGB color; //the RGB color value for the pixel
  int maxIterations = 300;//after how much iterations the function should stop

  //loop through every pixel
  for(int y = 0; y < h; y++)
  for(int x = 0; x < w; x++)
  {
    //calculate the initial real and imaginary part of z, based on the pixel location and zoom and position values
    pr = 1.5 * (x - w / 2) / (0.5 * zoom * w) + moveX;
    pi = (y - h / 2) / (0.5 * zoom * h) + moveY;
    newRe = newIm = oldRe = oldIm = 0; //these should start at 0,0
    //"i" will represent the number of iterations
    int i;
    //start the iteration process
    for(i = 0; i < maxIterations; i++)
    {
      //remember value of previous iteration
      oldRe = newRe;
      oldIm = newIm;
      //the actual iteration, the real and imaginary part are calculated
      newRe = oldRe * oldRe - oldIm * oldIm + pr;
      newIm = 2 * oldRe * oldIm + pi;
      //if the point is outside the circle with radius 2: stop
      if((newRe * newRe + newIm * newIm) > 4) break;
    }
    //use color model conversion to get rainbow palette, make brightness black if maxIterations reached
    color = HSVtoRGB(ColorHSV(i % 256, 255, 255 * (i < maxIterations)));
     //draw the pixel
     pset(x, y, color);
  }
  //make the Mandelbrot Set visible and wait to exit
  redraw();
  sleep();
  return 0;
}

Isn't that pretty:


Mandelbrot Explorer

Here's again the full code of a program that allows you to move around and zoom in the Mandelbrot Set.

int main(int argc, char *argv[])
{
  screen(320, 240, 0, "Mandelbrot Explorer");

  //each iteration, it calculates: new = old*old + c, where c is a constant and old starts at current pixel
  double pr, pi;           //real and imaginary part of the pixel p
  double newRe, newIm, oldRe, oldIm;   //real and imaginary parts of new and old
  double zoom = 1, moveX = -0.5, moveY = 0; //you can change these to zoom and change position
  ColorRGB color; //the RGB color value for the pixel
  int maxIterations = 128; //after how much iterations the function should stop

  double time, oldTime, frameTime; //current and old time, and their difference (for input)
  int showText = 0;

  //begin main program loop
  while(!done())
  {
    //draw the fractal
    for(int y = 0; y < h; y++)
    for(int x = 0; x < w; x++)
    {
      //calculate the initial real and imaginary part of z, based on the pixel location and zoom and position values
      pr = 1.5 * (x - w / 2) / (0.5 * zoom * w) + moveX;
      pi = (y - h / 2) / (0.5 * zoom * h) + moveY;
      newRe = newIm = oldRe = oldIm = 0; //these should start at 0,0
      //i will represent the number of iterations
      int i;
      //start the iteration process
      for(i = 0; i < maxIterations; i++)
      {
        //remember value of previous iteration
        oldRe = newRe;
        oldIm = newIm;
        //the actual iteration, the real and imaginary part are calculated
        newRe = oldRe * oldRe - oldIm * oldIm + pr;
        newIm = 2 * oldRe * oldIm + pi;
        //if the point is outside the circle with radius 2: stop
        if((newRe * newRe + newIm * newIm) > 4) break;
      }
      //use color model conversion to get rainbow palette, make brightness black if maxIterations reached
      color = HSVtoRGB(ColorHSV(i % 256, 255, 255 * (i < maxIterations)));
      //draw the pixel
      pset(x, y, color);
    }

    //print the values of all variables on screen if that option is enabled
    if(showText <= 1)
    {
      print("X:", 1, 1, RGB_White, 1); print(moveX, 17, 1, RGB_White, 1);
      print("Y:", 1, 9, RGB_White, 1); print(moveY, 17, 9, RGB_White, 1);
      print("Z:", 1, 17, RGB_White, 1); print(zoom, 17, 17, RGB_White, 1);
      print("N:", 1, 25, RGB_White, 1); print(maxIterations, 17, 25, RGB_White, 1);
    }
    //print the help text on screen if that option is enabled
    if(showText == 0)
    {
      print("Arrows move (X,Y), Keypad +,- zooms (Z)", 1, h - 25, RGB_White, 1);
      print("Keypad *,/ changes iterations (N)    ", 1, h - 17, RGB_White, 1);
      print("a to z=presets (qwerty), F1=cycle texts", 1, h - 9, RGB_White, 1);
    }
    redraw();

    //get the time and old time for time dependent input
    oldTime = time;
    time = getTicks();
    frameTime = time - oldTime;
    readKeys();
    //ZOOM keys
    if(keyDown(SDLK_KP_PLUS))  {zoom *= pow(1.001, frameTime);}
    if(keyDown(SDLK_KP_MINUS)) {zoom /= pow(1.001, frameTime);}
    //MOVE keys
    if(keyDown(SDLK_DOWN))  {moveY += 0.0003 * frameTime / zoom;}
    if(keyDown(SDLK_UP))  {moveY -= 0.0003 * frameTime / zoom;}
    if(keyDown(SDLK_RIGHT)) {moveX += 0.0003 * frameTime / zoom;}
    if(keyDown(SDLK_LEFT))  {moveX -= 0.0003 * frameTime / zoom;}
    //keys to change number of iterations
    if(keyPressed(SDLK_KP_MULTIPLY)) {maxIterations *= 2;}
    if(keyPressed(SDLK_KP_DIVIDE))   {if(maxIterations > 2) maxIterations /= 2;}
    //key to change the text options
    if(keyPressed(SDLK_F1)) {showText++; showText %= 3;}
  }
  return 0;
}

By moving around and zooming you can get very pretty pictures here. The parameter values were left on the pictures so you can see the coordinates, the zoom level and number of maximum iterations to generate those pictures:

This part of the Mandelbrot Set is called the Seahorse Valley:


A deeper zoom to the size of the Seahorse Valley (zoomed in 1779 times):


A detail on the other side of the set:


A few "minibrots", the first zoomed in only 8463 times, the second zoomed in 419622325484 times! Such minibrots only become visible if you allow enough iterations.


This is the effect of using more iterations: on the right is the same picture on the left, but with twice as much maximum iterations:


This is a deep zoom with a very high number of iterations in the side of the elephant valley. The elephant valley is the pointy shape on the X-axis, on right side of the mandelbrot.


This picture is added more recently, because it's pretty pretty:



And here's a picture that's zoomed in so much, that the numerical limit of 64-bit floating point numbers was reached. It starts looking blocky. It's zoomed in more than 10^18 times though, for deeper detail, processors with higher precision, or emulation of infinite precision numbers is required:


If you like, here's the link to a Mandelbrot Set of 1280*1024 pixels.

Last edited: 2004

Copyright (c) 2004-2007 by Lode Vandevenne. All rights reserved.