Lode's Computer Graphics Tutorial

Light and Color

Table of Contents

Back to Index

Introduction

This tutorial is about color, which is no doubt a very important aspect of computer graphics.

First is explained how light is built up and why we actually see different colors.

Then a some color models are explained: first the RGB color model used by computers, and examples showing how to do color arithmetics in RGB, and then the more intuitive HSL/HSV models are explained.

Then code is given that allows you to convert between color models, for example to allow a user to pick a color using the HSV color model and then convert it to RGB so the computer can use it, or to create rainbow gradients, or to change the color of images.

Light

Before starting about color models, it's important to know how the human eye and brain turn light into color.

Light itself is an electromagnetic wave. Electromagnetic waves are similar to sound waves in that they contain different frequencies, but are electromagnetic and can propagate in vacuum. EM waves are thus a signal that's made out of one or more frequencies, for example the EM waves used by a microwave oven are very high frequency, while radio waves are very low frequency. The eye is only sensitive to a very narrow band of frequencies, namely the frequencies between 429 THz and 750 THz (1 THz = 1 TeraHertz = 10^12 Hz). All other EM waves can't be seen.

Monochromatic light is light made up of one single pure frequency (this is certainly not the general case, most light you see is multichromatic). Monochromatic light looks to the eye as a pure color, and can never be white or magenta. Since it contains only one frequency, the wave of monochromatic light can be represented as a sine:



The height of the sine is the amplitude or how bright the light is. The width of one period (called lambda) is the wavelength of the light, and is inversely related to the frequency: since the light travels at 300000000 m/s, its wavelength is 300000000/f where f is the frequency. So the visible spectrum of light has wavelengths from around 400 to 700 nm.(1 nm = 10^-9 meter).



This visible spectrum shows all the possible colors that can be made out of monochromatic light. Some light sources, such as lasers and Natrium lights, send out monochromatic light, but in general, light is multichromatic. For example, the sun sends out white light, which is light that contains ALL frequencies! That means the sum of red, yellow, green, blue and violet light looks like white! Physically speaking, it's not white at all, it's the sum of a lot of sine curves, but the human brain makes it look white. Color is thus something psychologically, and not something physical.

Lightwaves are a sum of many different frequencies, or the sum of many sine curves. Each of these sine curves has its own frequency, and can have its own amplitude. A spectrum shows for each frequency the amplitude. For more information about spectra in general, see the beginnings of the chapter about Fourier Transforms.

Here's an example of such a spectrum:



It is the spectrum of a yellow LED I found. The top of the spectrum is the Dominant Frequency, and that is the color our eyes will usually see if light with this spectrum shines on it. If this yellow LED would have been monochromatic, the spectrum would have looked like this instead:



And to the eyes, the color would look the same. So here an interesting fact shows up: light with different spectra, can still look the same to the eye! If the human eyes would be able to distinguish every single spectrum as a different color, we would've been able to see gazillions of different colors, but the human eye works differently and turns a whole spectrum into only 3 signals: the amount of detected red, green and blue, and combinations of those make the colors we can see.

The spectrum of white light is as follows (the height of the curve doesn't really matter):



All frequencies are equally much in the light, only then it looks purely white to the brain. In all other cases, a certain frequency will be dominant and then that frequency will be the color the brain sees.

The spectrum of black light looks like this:



Indeed, there's no light at all, the amplitude of every frequency is zero. Black is the color the brain gives to the absence of light.

The spectrum of magenta, a color that can't be made with monochromatic light, could look like this:



Both blue and red have a high amplitude, and the mix of blue and red frequencies looks like magenta or purple to the brain.

The Eye and Color Perception

This section isn't about how the physical structure of the eye and the lens work, but about how the eye and the brain distinguish different colors.

So light falls on the retina, and on the retina are 2 types of cells with photosensitive chemicals, photoreceptors: rods and cones. The rods only detect whether or not light is present, and are important at night. So rods are sensitive to the whole spectrum at once and can't tell what frequency the light has, and thus can't provide any color information. To detect color, you'd need photoreceptors that are sensitive to only a certain frequency. That's exactly what the cones do:

There are 3 types of cones, those that are sensitive to red, those sensitive to green, and those sensitive to blue. Such a rod isn't sensitive to a single frequency, they overlap a bit, it's just sensitive mostly to a certain frequency.

For example, yellow has a frequency between red and green. This yellow frequency will excite both the red and green cones a bit, and the human brain converts the signal "both red and green cones are excited" to "yellow". Even the blue cones are still a bit excited by yellow light, but neglectable.

If light falls on the eye that has two frequencies: red and green, it'll also excite both the red and green cones, so this light will show up as yellow as well, even though it doesn't contain any yellow frequency at all.

If blue light falls on the retina, the blue cones are excited very strongly, while the green and red ones will give only a neglectable signal. And the brain turns the signal "mainly the blue cone is excited" to "blue".

White light contains all frequencies, so if white light falls on the retina, all 3 types of cones are excited, and the brain turns the signal "green, red and blue cones all excited" into "white".

The above explains how the brain creates different "hues" of colors out of the incoming signal, but it also gives a certain brightness to the light, based on how strong the incoming signal is: if it's very strong, the brain indicates it as a very bright red, white, ..., but if it's very weak, it'll be almost black. And then there's also the "saturation" of the color, this is based on the relative difference in strength each color type gives: if the red signal is very strong, but blue and green are also pretty strong, the color will have a low saturation, it's red-grayish or red-whitish. If however the red signal would be very strong, and the blue and green signal very weak, a very red color shows up.

Since different spectra can look exactly the same for us, and some animals have different types of color receptors, it's possible that two colors that look the same to us, look like two different colors for some animal.

The above process happens on every location of the retina separately, so that a complex 2-dimensional image is formed where each location on the image can have its own color.

Thanks to the 3 types of cones, there are 8 (2^3) main colors one can distinguish:

You can of course distinguish much more colors than these 8 because each receptor type can have different levels of excitement.

Color blindness means one or more of the color types of cones are missing or less sensitive, for example if you miss the red one, you can only see the difference between light that has mainly green and light that has mainly blue. Light with mainly red, will show up as green for such a person, because the green receptors are still more sensitive to red than the blue ones. People who have 2 types of cones missing, and have thus only one type left, see in black and white, because only two main types of signals now exist: "the cone is excited" and "the cone is not excited". Imagine how much more colors a human would be able to see if he had 4 types of color receptors instead of only 3.

One final question remains: violet is on one side of the spectrum, while red is totally on the other side. Violet is much closer to the blue receptors of the eye than the red ones, so you'd think violet light would look like pure blue to the eye. But violet looks a bit more like purple, hinting that it has some red in it, why could that be?



The reason is that violet has such a high frequency, too high for the blue receptor as well, that the signal is very weak for both the blue and the red receptor. Relatively speaking, the red and blue signal will thus be pretty close to each other, and the color will show up more like purple than like blue for the brain!

The RGB Color Model

The RGB color model works exactly like those color receptors of the human eye work: the RGB color model describes a color by using 3 variables, Red, Green and Blue. These variables can be compared to the strength of the signals from the 3 types of color receptors in the nerves. A computer or TV screen works this way too: it has 3 types of cells, Red, Green and Blue, and can make each type brighter or darker independently, exciting the correct receptors of the eye to create the desired color. If you look with a magnifying glass to a white area of your computer screen, you can see that the color white is actually made out of the 3 colors red, green and blue. This means the white emitted by a computer screen is different from white sunlight: while white sunlight contains photons of all frequencies (except a few), the computer screen only has 3 frequencies. The human eye can't see the difference between these two kinds of white.

The RGB color model is the one you'll mostly be dealing with in computer graphics. It's also called the additive color model, because you add 3 color components together to form any color. In 24-bit color, each of the 3 components R, G and B is an 8-bit variable that can be an integer number between 0 and 255. 0 means the color component is off (black), while 255 means it's at its full intensity. 127 is half intensity. This means color 0,0,0 is the darkest black, color 255,0,0 is the brightest red, color 0,255,0 is the brightest green and color 0,0,255 is the brightest blue. 255,255,255 is the brightest white and 127,127,127 is gray. 32-bit color is the same but with an extra 8-bit alpha channel added that can be used for transparency of textures, ...

The RGB color model isn't very intuitive, so here's a table containing some common RGB values:

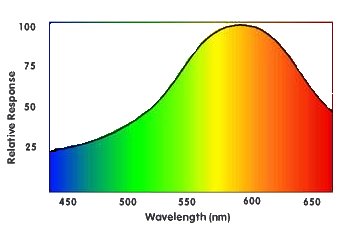
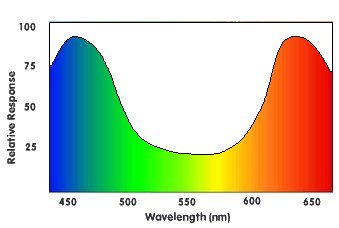
Here is a table with common RGB color values:

R G B Hex Value
 Color
0 0 0 000000 Black
255 0 0 FF0000 Red
0 255 0 00FF00 Green
0 0 255 0000FF Blue
255 255 0 FFFF00 Yellow
255 0 255 FF00FF Magenta
0 255 255 00FFFF Cyan
255
 128
 128
 FF8080
 Bright Red
128
 255
 128
 80FF80
 Bright Green
128
 128
 255
 8080FF
 Bright Blue
64 64 64 404040 Dark Grey
128 128 128 808080 Intermediate Grey
192 192 192 C0C0C0 Bright Grey
255 255 255 FFFFFF White

This way, you should be able to guess that 128,0,0 is dark red, 255,128,192 is pink and 16,16,16 is very dark gray. The Hex value is the hexadecimal code of the color, used for example in HTML.

The R, G and B values are the ones to fill in as parameters for functions of QuickCG like pset, drawLine, drawCircle to give the color.

In RGB color, the higher the values of R, G and B, the brighter the color will be, and if R=G=B, the color will be a shade of gray.

If you set R=x, G=y, B=z, you can represent RGB color on a cube, where the origin is black and the corner at R=255,G=255,B=255 is white:

RGB Arithmetic

By doing calculations on the RGB values of the pixels of an image you can perform various color effects.

Here's a table of the operations you can do with RGB color, screenshots and code will follow in the next sections. These operations are given for the 24-bit color model with 8 bit per channel, so 255 is the maximum value of a color. Colors channels can also be represented as floating point numbers between 0.0 and 1.0, then you have to replace the value "255" by "1.0". C represents the channel together or the total color, while R, G and B represent the Red, Green and Blue channel separately.

Operation
 Formula
 Effect
Negative
 255-C
 Returns the opposite color, for example white becomes black, red becomes cyan, ...
Darken
 C/p or C-p
 Divide the color though some constant (larger than 1), or subtract a constant from it, to make it darker.
Brighten
 C*p or C+p
 Multiply the color by some constant (larger than 1), or add a constant to it, to make it brighter.
Greyscale
 0.2126 * R + 0.7152 * G + 0.0722 * B
 Calculate a weighed average (here based on ITU Rec.709) of the 3 channels to get a gray color with the same brightness.
Remove Channel
 R=0, G=0 and/or B=0
 By setting one or more channels to 0, you completely remove that color component from the picture.
Swap Channels
 R=G, G=R, ...
 Swap the values of two color channels to get an image with a completely different color.

We'll try all these formulas on the following PNG image of a flower:


Negative Image

The following code will load a PNG image of 200*133 pixels, calculate its negative, and display the result. ColorRGB is the struct containing 3 integers r, g and b, to describe the rgb color.

int main(int argc, char *argv[])
{
  unsigned long w = 0, h = 0;
  std::vector<ColorRGB> image;
  loadImage(image, w, h, "pics/flower.png");
  screen(w, h, 0, "RGB Color");

  ColorRGB color; //the color for the pixels

  for(int y = 0; y < h; y++)
  for(int x = 0; x < w; x++)
  {
    //here the negative color is calculated!
    color.r = 255 - image[y * w + x].r;
    color.g = 255 - image[y * w + x].g;
    color.b = 255 - image[y * w + x].b;
    pset(x, y, color);
  }

  redraw();
  sleep();
  return 0;
}

image[y * w + x].r is the red component of pixel x, y of the image, so 255 - image[y * w + x].r is the negative of it. This is done for each color channel. Here's the result:



You could as well have typed "color = RGB_White - image[y * w + x]" instead of the 3 lines of code, because the ColorRGB struct supports a few operators.

Change the Brightness

To change the brightness, divide R, G and B through a number larger than 1 to make it darker, or multiply them with that number to make it brighter. If the color component becomes higher than 255, truncate it to 255.

For example, to make the image double as dark, change the 3 lines of code that made the image negative in the previous example, to:


        color.r = image[y * w + x].r / 2;
        color.g = image[y * w + x].g / 2;
        color.b = image[y * w + x].b / 2;



Or to make it 1.5 times as dark, use:

        color.r = int(image[y * w + x].r / 1.5);
        color.g = int(image[y * w + x].g / 1.5);
        color.b = int(image[y * w + x].b / 1.5);



To make it twice as bright, use:

        color.r = image[y * w + x].r * 2;
        color.g = image[y * w + x].g * 2;
        color.b = image[y * w + x].b * 2;

        if(color.r > 255) color.r = 255;
        if(color.g > 255) color.g = 255;
        if(color.b > 255) color.b = 255;



Instead of dividing or multiplying, you can also add or subtract a number instead, this even gives better results when making it brighter:

        color.r = image[y * w + x].r + 50;
        color.g = image[y * w + x].g + 50;
        color.b = image[y * w + x].b + 50;

        if(color.r > 255) color.r = 255;
        if(color.g > 255) color.g = 255;
        if(color.b > 255) color.b = 255;



Or darker:

        color.r = image[y * w + x].r - 50;
        color.g = image[y * w + x].g - 50;
        color.b = image[y * w + x].b - 50;

        if(color.r < 0) color.r = 0;
        if(color.g < 0) color.g = 0;
        if(color.b < 0) color.b = 0;



Greyscale

One way to grayscale an image is to calculate a weighed average (here based in ITU Rec. 709) of the 3 color components and use this average as the value for the shade of gray. The eye is less sensitive to blue, so it gets a smaller coefficient, and more to green so it gets a larger one:

        color.r = color.g = color.b = 0.2126 * image[y * w + x].r + 0.7152 * image[y * w + x].g + 0.0722 * image[y * w + x].b;



Swapping and Removing Channels

By removing channels, you completely remove a color of the image, for example if you remove the red of the flower you get this:

        color.r = 0;
        //red component set to zero
        color.g = image[y * w + x].g;
        color.b = image[y * w + x].b;



If you remove green instead, you get:



And if you remove blue, you get:



The last image looks quite similar to the original because there wasn't much blue in the image, though white areas now look green or yellow, and everything has become a bit darker.

Swapping two channels can give results with a totally different color, for example if we swap the red and green channel the flower becomes green while the background becomes reddish:

        color.r = image[y * w + x].g; //the green component of the image
        color.g = image[y * w + x].r; //the red component of the image
        color.b = image[y * w + x].b; //the blue component of the image



And if red and blue are swapped instead, the flower becomes of course blue:



To make the flower yellow, set both R and G to the red channel of the image:

        color.r = image[y * w + x].r; //the red component of the image
        color.g = image[y * w + x].r; //the red component of the image
        color.b = image[y * w + x].b; //the blue component of the image



The HSL Color Model

HSL is another way to describe color with 3 parameters. RGB is the way computer screens work, but not very intuitive. HSL is more intuitive, but you need to convert it to RGB before you can draw a pixel with it. The nicest application of this color model is that you can easily create rainbow gradients or change the color, lightness or saturation of an image with this color model.

HSL color obviously has the parameters H, S and L, or Hue, Saturation and Lightness.

Hue indicates the color sensation of the light, in other words if the color is red, yellow, green, cyan, blue, magenta, ... This representation looks almost the same as the visible spectrum of light, except on the right is now the color magenta (the combination of red and blue), instead of violet (light with a frequency higher than blue):



Hue works circular, so it can be represented on a circle instead. A hue of 360° looks the same again as a hue of 0°.



Saturation indicates the degree to which the hue differs from a neutral gray. The values run from 0%, which is no color, to 100%, which is the fullest saturation of a given hue at a given percentage of illumination. The more the spectrum of the light is concentrated around one wavelength, the more saturated the color will be.



Lightness indicates the illumination of the color, at 0% the color is completely black, at 50% the color is pure, and at 100% it becomes white. In HSL color, a color with maximum lightness (L=255) is always white, no matter what the hue or saturation components are. Lightness is defined as (maxColor+minColor)/2 where maxColoris the R, G or B component with the maximum value, and minColor the one with the minimum value. Please note that the lightness of HSL and HSV is not a good approximation of the actual perceived lightness, a linear combination such as 0.2126*R + 0.7152*G + 0.0722*B or 0.299*R + 0.587*G + 0.114*B is more precise. HSL and HSV are easy to use color models but do not attempt to model the human visual system well. See the end of this tutorial for other color models.



In this tutorial, Hue, Saturation and Lightness will be presented as numbers between 0-255 instead, so that the HSL model has the same 24 bits as the RGB model.

The HSL color model is for example used in Paint Shop Pro's color picker.

The HSV Color Model

The HSV color model (sometimes also called HSB), uses the parameter Value instead of Lightness. Value works different than Lightness, in that the color with maximum value (V=255) can be any color like red, green, yellow, white, etc..., at its maximum brightness. Value is defined as maxColor, where maxColor is the R, G or B component with the maximum value. So the colors red (255,0,0) and white (255,255,255) both have a Value of 255 indeed.

In HSL, the Lightness showed the following behavior when increased:



In HSV, Value does the following:



The Hue and Saturation parameters work very similar to the ones in HSL. HSV is generally better at representing the saturation, while HSL is better at representing the brightness. However, HSV is again better to decrease the brightness of very bright images.

We can compare the HSL and HSV model a bit better by comparing their plots:

Here is the plot of HSL (left) and HSV (right) with S=255, Hue on the horizontal axis, and Lightness/Value on the vertical axis (maximum lightness at the top):



While the top of the HSL curve is white because white is the color with maximum brightness, the top of the HSV curve contains all colors, because the saturation is 255 and in HSV, saturation 255 has to be a color while white should have 0 saturation. The top of the HSV curve is the same as the center horizontal line of the HSL curve, and the complete HSV curve is exactly the same as the bottom half of the HSL picture.

Here is the plot of HSL (left) and HSV (right) with L=255 and V=255 respectively, Hue on the horizontal axis, and Saturation on the vertical axis (maximum saturation at the bottom):



The HSL curve is completely white, because white is the only color with L=255 in the HSL model. The HSV curve, now shows all colors that have one or more of their color components equal to 255. The HSV picture here, is exactly the same as the top half of the previous HSL picture where S=255.

And here's the plot of HSL (left) and HSV (right) with L=128 and V=128 respectively, and again Hue on the horizontal axis, and Saturation on the vertical axis (maximum saturation at the bottom):



Color Model Conversions

To draw the plots given above, color model conversion functions have to be used: first you describe the color as HSL or HSV, but to plot it on screen, it has to be converted to RGB first. Transformations from RGB to HSL/HSV are handy as well, for example if you load an RGB image and want to change it hue, you have to convert it to HSL or HSV first, then change the hue, and then change it back to RGB.

The color model conversion formulas are already in QuickCG, in the QuickCG.cpp file.

RGB to HSL

The following function converts from RGB color to HSL color. You give it a ColorRGB and it returns a ColorHSL. Both ColorRGB and ColorHSL are simple structs with 3 integers, the only difference is their names. The RGBtoHSL function calculates the values for ColorHSL.

First the variables r, g, b, h, s, l are declared as floating point numbers. Internally, the function works with floating point numbers between 0.0 and 1.0, for better precision. At the end of the function, the results can very easily be converted back to integers from 0-255. The function can also easily be modified to work with other ranges, e.g. if you'd want to use 16 bit per color channel, or represent Hue as a value between 0° and 360°.

ColorHSL RGBtoHSL(ColorRGB colorRGB)
{
    float r, g, b, h, s, l; //this function works with floats between 0 and 1
    r = colorRGB.r / 256.0;
    g = colorRGB.g / 256.0;
    b = colorRGB.b / 256.0;

Then, minColor and maxColor are defined. Mincolor is the value of the color component with the smallest value, while maxColor is the value of the color component with the largest value. These two variables are needed because the Lightness is defined as (minColor + maxColor) / 2.

    float maxColor = max(r, max(g, b));
    float minColor = min(r, min(g, b));

If minColor equals maxColor, we know that R=G=B and thus the color is a shade of gray. This is a trivial case, hue can be set to anything, saturation has to be set to 0 because only then it's a shade of gray, and lightness is set to R=G=B, the shade of the gray.

    //R == G == B, so it's a shade of gray
    {
        h = 0.0; //it doesn't matter what value it has
        s = 0.0;
        l = r; //doesn't matter if you pick r, g, or b
    }

If minColor is not equal to maxColor, we have a real color instead of a shade of gray, so more calculations are needed:


    else
    {
        l = (minColor + maxColor) / 2;

        if(l < 0.5) s = (maxColor - minColor) / (maxColor + minColor);
        else s = (maxColor - minColor) / (2.0 - maxColor - minColor);

        if(r == maxColor) h = (g - b) / (maxColor - minColor);
        else if(g == maxColor) h = 2.0 + (b - r) / (maxColor - minColor);
        else h = 4.0 + (r - g) / (maxColor - minColor);

        h /= 6; //to bring it to a number between 0 and 1
        if(h < 0) h ++;
    }

Finally, H, S and L are calculated out of h,s and l as integers between 0 and 255 and "returned" as the result. Returned, because H, S and L were passed by reference to the function.

    ColorHSL colorHSL;
    colorHSL.h = int(h * 255.0);
    colorHSL.s = int(s * 255.0);
    colorHSL.l = int(l * 255.0);
    return colorHSL;
}

HSL to RGB

This is the opposite conversion, so this function will calculate the inverse of the RGBtoHSL function.

First, internally the variables with small letters are defined as floating point numbers between 0 and 1 again. Some temporary values for the calculations are also declared.

ColorRGB HSLtoRGB(ColorHSL colorHSL)
{
    float r, g, b, h, s, l; //this function works with floats between 0 and 1
    float temp1, temp2, tempr, tempg, tempb;
    h = colorHSL.h / 256.0;
    s = colorHSL.s / 256.0;
    l = colorHSL.l / 256.0;

Then follows a trivial case: if the saturation is 0, the color will be a grayscale color, and the calculation is then very simple: r, g and b are all set to the lightness.

    //If saturation is 0, the color is a shade of gray
    if(s == 0) r = g = b = l;

If the saturation is higher than 0, more calculations are needed again. red, green and blue are calculated with the formulas defined in the code.

    //If saturation > 0, more complex calculations are needed
    else
    {
        //Set the temporary values
        if(l < 0.5) temp2 = l * (1 + s);
        else temp2 = (l + s) - (l * s);
        temp1 = 2 * l - temp2;
        tempr = h + 1.0 / 3.0;
        if(tempr > 1) tempr--;
        tempg = h;
        tempb = h - 1.0 / 3.0;
        if(tempb < 0) tempb++;

        //Red
        if(tempr < 1.0 / 6.0) r = temp1 + (temp2 - temp1) * 6.0 * tempr;
        else if(tempr < 0.5) r = temp2;
        else if(tempr < 2.0 / 3.0) r = temp1 + (temp2 - temp1) * ((2.0 / 3.0) - tempr) * 6.0;
        else r = temp1;

        //Green
        if(tempg < 1.0 / 6.0) g = temp1 + (temp2 - temp1) * 6.0 * tempg;
        else if(tempg < 0.5) g = temp2;
        else if(tempg < 2.0 / 3.0) g = temp1 + (temp2 - temp1) * ((2.0 / 3.0) - tempg) * 6.0;
        else g = temp1;

        //Blue
        if(tempb < 1.0 / 6.0) b = temp1 + (temp2 - temp1) * 6.0 * tempb;
        else if(tempb < 0.5) b = temp2;
        else if(tempb < 2.0 / 3.0) b = temp1 + (temp2 - temp1) * ((2.0 / 3.0) - tempb) * 6.0;
        else b = temp1;
    }

And finally, the results are returned as integers between 0 and 255.

    ColorRGB colorRGB;
    colorRGB.r = int(r * 255.0);
    colorRGB.g = int(g * 255.0);
    colorRGB.b = int(b * 255.0);
    return colorRGB;
}

RGB to HSV

The function RGBtoHSV works very similar as the RGBtoHSL function, the only difference is that now the variable V (Value) instead of L (Lightness) is used, and Value is defined as maxColor. This can immediately be calculated at the beginning of the function:

ColorHSV RGBtoHSV(ColorRGB colorRGB)
{
    float r, g, b, h, s, v; //this function works with floats between 0 and 1
    r = colorRGB.r / 256.0;
    g = colorRGB.g / 256.0;
    b = colorRGB.b / 256.0;
    float maxColor = max(r, max(g, b));
    float minColor = min(r, min(g, b));
    v = maxColor;

Then, the saturation is calculated. If the color is black, the value of saturation doesn't matter so it can be set to 0. This has to be done to avoid a division by zero.

    if(maxColor == 0) //avoid division by zero when the color is black
    {
        s = 0;
    }
    else
    {
        s = (maxColor - minColor) / maxColor;
    }

Finally, the hue is calculated. If saturation is 0, the color is gray so hue doesn't matter. Again this case is handled separately to avoid divisions by zero.

    if(s == 0)
    {
        h = 0; //it doesn't matter what value it has
    }
    else
    {
        if(r == maxColor) h = (g - b) / (maxColor-minColor);
        else if(g == maxColor) h = 2.0 + (b - r) / (maxColor - minColor);
        else h = 4.0 + (r - g) / (maxColor - minColor);
        h /= 6.0; //to bring it to a number between 0 and 1
        if (h < 0) h++;
    }

And finally, the results are returned as integers between 0 and 255.

    ColorHSV colorHSV;
    colorHSV.h = int(h * 255.0);
    colorHSV.s = int(s * 255.0);
    colorHSV.v = int(v * 255.0);
    return colorHSV;
}

HSV to RGB

First the floating point numbers between 0 and 1 are declared again:

ColorRGB HSVtoRGB(ColorHSV colorHSV)
{
    float r, g, b, h, s, v; //this function works with floats between 0 and 1
    h = colorHSV.h / 256.0;
    s = colorHSV.s / 256.0;
    v = colorHSV.v / 256.0;

The trivial case for saturation = zero is handled:

    //If saturation is 0, the color is a shade of gray
    if(s == 0) r = g = b = v;

The HSV model can be presented on a cone with hexagonal shape. For each of the sides of the hexagon, a separate case is calculated:

    //If saturation > 0, more complex calculations are needed
    else
    {
        float f, p, q, t;
        int i;
        h *= 6; //to bring hue to a number between 0 and 6, better for the calculations
        i = int(floor(h));  //e.g. 2.7 becomes 2 and 3.01 becomes 3 or 4.9999 becomes 4
        f = h - i;  //the fractional part of h
        p = v * (1 - s);
        q = v * (1 - (s * f));
        t = v * (1 - (s * (1 - f)));
        switch(i)
        {
            case 0: r = v; g = t; b = p; break;
            case 1: r = q; g = v; b = p; break;
            case 2: r = p; g = v; b = t; break;
            case 3: r = p; g = q; b = v; break;
            case 4: r = t; g = p; b = v; break;
            case 5: r = v; g = p; b = q; break;
        }
    }

And again, the results are "returned" as integers between 0 and 255.

    ColorRGB colorRGB;
    colorRGB.r = int(r * 255.0);
    colorRGB.g = int(g * 255.0);
    colorRGB.b = int(b * 255.0);
    return colorRGB;
}

HSL and HSV Arithmetic

The functions given above are already in the QuickCG, and thanks to them we can do HSL and HSV arithmetic on images.

The examples will be performed on the flower image again:



Changing Hue

It doesn't matter if you change hue with the HSL or HSV model, the results are the same, so for no particular reason at all let's do it with HSL here.

The following code will load the PNG image, convert it to HSL, change the Hue by adding a certain value to it, and convert it back to RGB to display it (put this code in the main function in the main.cpp file):

int main(int argc, char *argv[])
{
    ColorRGB colorRGB;
    ColorHSL colorHSL;

    unsigned long w, h;
    std::vector<ColorRGB> image;
    loadImage(image, w, h, "pics/flower.png");
    screen(w, h, 0, "RGB Color");

    for(int y = 0; y < h; y++)
    for(int x = 0; x < w; x++)
    {
        //store the color of the image in variables R, G and B
        colorRGB = image[y * w + x];
        //calculate H, S and L out of R, G and B
        colorHSL = RGBtoHSL(colorRGB);
        //change Hue
        colorHSL.h += int(42.5 * 1);
        colorHSL.h %= 255;
        //convert back to RGB
        colorRGB = HSLtoRGB(colorHSL);
        //plot the pixel
        pset(x, y, colorRGB);
    }
    redraw();
    sleep();
    return 0;
}

The Hue is modulo divided through 255, because it has to be between 0 and 255, and it's circular, so a hue of 260 is the same as a hue of 5. The value 42.5 was chosen to be 255/6, representing a hue shift of 60°. Here are screenshots of the result for a hue shift of 0°, 60°, 120°, 180°, 240° and 300° (360° gives the same result as 0° again):





You can also set Hue to a constant, to give the whole image the same color. For example, here hue is set to 25, which is orange:



Changing Saturation

You can change the saturation to make the image more colorful, or more like pastel, or grayscale. This time, the results are slightly different if you use the HSL or HSV color model.

For example, to increase the saturation by multiplying it with 2.5, change the lines of the code that changed the hue to:

    colorHSV.s = int(colorHSV.s * 2.5);
    if(colorHSV.s > 255) colorHSV.s = 255;

If Saturation is higher than 255, it's truncated. On the left is the result if you use HSL, on the right if you use HSV. The result is pretty similar to the original image because the saturation in it was quite high already. Only the background became a bit more green.



If you multiply it with 0.5 instead, you'll decrease the saturation by halving it:



You can also decrease the saturation by substracting a value from it instead:

    colorHSV.s = colorHSV.s - 100;
    if(colorHSV.s < 0) colorHSV.s = 0;

The background will be grayscale now, while the flower with its high saturation still has some color:



If saturation is set to 0, the image will be grayscale, in a different way if you use HSL or HSV, and both are also different from the "average" formula to grayscale an image:



And this is what you get if you set saturation equal to 128 for all pixels. The flower and background look equally colorful now:



Changing Brightness

Finally, HSL and HSV can also be used to change the brightness of an image. Again, the HSL and HSV model will work differently. HSL gives bad result when making an image with white or near white pixels darker.



You can also decrease the saturation by substracting a value from it instead:

    colorHSV.l -= 50;
    if(colorHSV.l < 0) colorHSV.l = 0;

Here's the result for HSL on the left and HSV on the right:



And setting brightness equal to 192 for all pixels gives:



Gammma Correction

Gamma correction is done by raising the components to a power, but scaled to range 0-1 instead of 0-255, producing a new value in range 0-1. For typical computer monitors, the value of the power is, roughly speaking, 2.2. When color values correspond to the amount of light, this is called "linear" RGB color. However, in images, the color is usually not stored in the linear format, but gamma compressed with a power of 1 / 2.2. This works because computer screens do the opposite transform automatically, having the effect of raising to a power 2.2.

When doing operations on the pixels of an image, for correctness, these should be done in linear RGB, not compressed RGB, otherwise the non-linear color values affect your intended linear or other transformation (e.g. averaging two neighboring pixels). The rest of these tutorials actually forgot this fact (e.g. the one about filtering), but it's something to take into account in real worls applications.

So, to convert from compressed RGB to linear RGB, before doing operations: 

        color.r = 255.0 * std::pow(image[y * w + x].r / 255.0, 2.2);
        color.g = 255.0 * std::pow(image[y * w + x].g / 255.0, 2.2);
        color.b = 255.0 * std::pow(image[y * w + x].b / 255.0, 2.2);

And to convert back: 

        image[y * w + x].r = 255.0 * std::pow(color.r / 255.0, 1 / 2.2);
        image[y * w + x].g = 255.0 * std::pow(color.g / 255.0, 1 / 2.2);
        image[y * w + x].b = 255.0 * std::pow(color.b / 255.0, 1 / 2.2);


Other Color Models

This article focused on the RGB, HSL and HSV color models. However, there are a lot more, with various professional applications, such as television, publishing, data compression, ... In addition, careful math is required, and aspects have to be taken into account such as: gamma correction (mentioned above), the whitepoint, the human visual system, color gamut, chromaticity diagram... This is however beyond the scope of this tutorial. Working with these color spaces is best done with floating point numbers, using byte values 0-255 would cause loss of precision.

A good resource with exact math is Bruce Lindeboom's website: http://www.brucelindbloom.com/.

We'll finish with a brief list of some other color models, without providing conversion formulas here.


Last edited: 2004

Copyright (c) 2004-2007 by Lode Vandevenne. All rights reserved.