Lode's Computer Graphics Tutorial

Recursion Trees

Table of Contents

Back to Index

Introduction

Fractals have the property of self-similarity. One type of figure that fulfills this requirement, are Recursion Trees. The idea is as follows: you draw the stem of the tree, then the stem splits into two smaller branches, each of these two branches again splits into two smaller branches, etc... until infinity.

Recursion Tree with Two Branches

To code such a recursion tree, we need of course a recursive function. This function will draw one branch, and call itself again to draw two new branches, and since it has called itself again, these two called versions will again call itself again, etc... The parameters are changed each time to draw the branch at the correct position, with the correct angle and size. There's also a stop condition, it'll stop after n recursions, otherwise the calculation would never be finished and it'd end up in an infinite loop. In the nth step of recursion, 2^n branches have to be drawn.

First, some variables and the recursive function are declared. "pi" can be used to give your favorite angle in radians more easily. "maxRecursions" is for the stop condition of the recursive functions. "angle" is a constant, it's the angle each new branch will have compared to its parent branch. "shrink" is how much smaller each new branch is compared to its parent branch. You can change their values, the values here have been chosen to give one of the many possible nice results.

double pi = 3.1415926535897932384626433832795;

int maxRecursions = 8; //never make this too big or it'll take forever
double angle = 0.2 * pi; //angle in radians
double shrink = 1.8; //relative size of new branches

void recursion(double posX, double posY, double dirX, double dirY, double size, int n);

The main function doesn't do much more than setting up the screen, and then calling the recursive function. The value "h/2.3" in the parameters of the recursion function is the initial length of the first branch (the stem). The coordinates are the begin point and direction vector of the first branch.

int main(int argc, char *argv[])
{
  screen(320, 240, 0, "Recursion Tree");
  cls(RGB_White); //make background white

  //Now the recursion function takes care of the rest
  recursion(w / 2, h - 1, 0, -1, h / 2.3, 0);

  redraw();
  sleep();
  return 0;
}

Now follows the recursion function, a function that only draws a single line and calls itself a few times, but results in a huge tree!

Here's the part that draws the line. First the line is clipped to the screen, then drawn. The line is drawn from (posX, posY) to (posX+dirX, posY+dirY). So the position and direction of the line is given as a vector, instead of a begin point, an angle and a size, because direction vectors are much easier to work with. The size parameter itself isn't used to draw the line directly, it's only needed later to calculate the direction vector of the next branches. If the maximum number of recursions is needed, the function returns immediately after drawing the line, without calling itself again.

void recursion(double posX, double posY, double dirX, double dirY, double size, int n)
{
  int x1, x2, y1, y2;
  int x3, x4, y3, y4;
  x1 = int(posX);
  y1 = int(posY);
  x2 = int(posX + size * dirX);
  y2 = int(posY + size * dirY);
  if(clipLine(x1, y1, x2, y2, x3, y3, x4, y4))
  drawLine(x3, y3, x4, y4, ColorRGB(128, 96, 64));

  if(n >= maxRecursions) return;

And in the second part of the function, the new position of the new branches is calculated as the endpoint of the previous branch, and the new direction vector for the new branches is calculated out of the size and current direction of the current branch. The new branches are rotated with the angle, the sine and cosine formulas are actually the calculation of the rotation matrix. Then the recursion function is called again with the new branch in its parameters. This is done twice: once for a branch rotated to the right, and then for a branch rotated to the left.

  double posX2, posY2, dirX2, dirY2, size2;
  int n2;
  posX2 = posX + size * dirX;
  posY2 = posY + size * dirY;
  size2 = size / shrink;
  n2 = n + 1;
  dirX2 = cos(angle) * dirX + sin(angle) * dirY;
  dirY2 = -sin(angle) * dirX + cos(angle) * dirY;
  recursion(posX2, posY2, dirX2, dirY2, size2, n2);
  dirX2 = cos(-angle) * dirX + sin(-angle) * dirY;
  dirY2 = -sin(-angle) * dirX + cos(-angle) * dirY;
  recursion(posX2, posY2, dirX2, dirY2, size2, n2);
}

The result looks like this:



It's very easy to make the screen bigger, just change the parameters in the screen function, all the rest of the code is made relative to the size of the screen.

Here's an alternative main function, that will redraw the tree all the time with a different angle.

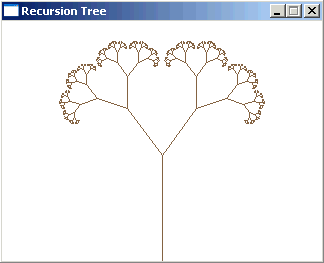
int main(int argc, char *argv[])
{
  screen(320, 240, 0, "Recursion Tree");
  while(!done())
  {
    angle = getTicks() / 2000.0;
    cls(RGB_White);
    recursion(w / 2, h - 1, 0, -1, h / 2.3, 0);
    redraw();
  }
  return 0;
}

The angle is set to the time divided through some factor determining the speed of the animation. Here are a few of the results you get for different angles:


Recursion Tree with More Branches

Instead of only 2 branches, you can also give it more branches of course. For example, to give it 3 branches, let the recursive function call itself 3 times instead of only 2. This gives a huge increase in complexity however: now, if n is the max number of recursions, the number of branches to draw will be 3^n only in the last step, so if n=8, that's 6561 branches!

It isn't difficult to extend to 3 or more branches, you just have to choose a nice angle for the new branches. The following code also has something extra: at the end of each branch, a green circle will be painted, making it look like leaves. It also allows to turn on or off  up to 4 branches separately, and give each branch a fixed or time varying angle. In the main function are different input keys that create different angles and settings.

Everything is declared again, the explanation of each variable is in the comments. The angle of branch i will be angle*ai+ci, where angle varies with the time.

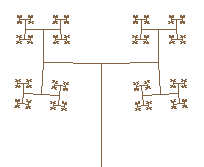
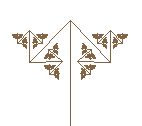
double pi = 3.1415926535897932384626433832795;

int maxRecursions = 6; //max number of recursions
double angle; //angle in radians, this parameter changes with time
bool enable1, enable2, enable3, enable4; //enable or disable up to 4 branches
double a1, a2, a3, a4, c1, c2, c3, c4; //angle multipliers and adders for those 4 branches
double size, shrink; //the size of the first branch, and the relative size of the next ones

bool releaseSpace; //for input
int drawLeaves = 4; //what type of leaves to draw, if any

void recursionTree(double posX, double posY, double dirX, double dirY, double size, int n);

In the main function, some initial parameters are set, and then the while loop starts. This while loop will draw the tree each time and change the angle a with the time.

int main(int argc, char *argv[])
{
  screen(512, 384, 0, "Recursion Tree");

  //Initial settings
  enable1 = 1; enable2 = 1; enable3 = 1; enable4 = 0; //1 enables, 0 disables branch
  a1 = 1.0; a2 = -1.0; a3 = 0.0; a4 = 0.0; //how fast the angles rotate
  c1 = 0.0; c2 = 0.0; c3 = 0.2; c4 = 0.0; //absolute angle
  size = h / 3; //size of the first branch (the stem)
  shrink = 1.5; //relative size of the new branch

  while(!done())
  {
    angle = getTicks() / 3000.0;
    cls(RGB_White);
    recursionTree(w / 2, h - 1, 0, -1, size, 0); //This function will draw a single line and call itself a few times, creating a tree
    redraw();

	//Presets of settings
    readKeys();

The second part of the loop changes the settings like the angles, the number of recursions, ... according to some presets. It's easy to change them or add more if you like. The releaseSpace variable is used for the space key: it's there so that if you press the space key, it'll only change the setting again after you released the space key again.

    if(keyPressed(SDLK_a)) {enable1 = enable2 = enable3 = 1; enable4 = 0;a1 =1;a2 = -1; a3 = 0;c1 = c2 = 0; c3 = 0.2; size = h / 3; shrink = 1.5; maxRecursions = 6;} //default one with rotating branches
    if(keyPressed(SDLK_b)) {enable1 = enable2 = enable3 = 1; enable4 = 0;a1 = a2 =a3 = 0; c1 = 0;c2 = 2 * pi / 3; c3 = -2 * pi / 3; size = h / 2; shrink = 2; maxRecursions = 8;} //sierpinski triangle
    if(keyPressed(SDLK_c) {enable1 = enable2 = enable3 = enable4=1; a1 = a2 = a3 = a4 = 0; c1 = 0; c2 = pi / 2; c3 = pi; c4 = -pi / 2; size = h / 2; shrink = 2; maxRecursions = 6;}  //square
    if(keyPressed(SDLK_d) {enable1 = enable2 = enable3 = 1; enable4 = 0;a1 = a2 = a3 = 0; c1 = 0; c2 = pi / 2; c3 = -pi / 2; size = h / 2; shrink = 2; maxRecursions = 8;} //90?
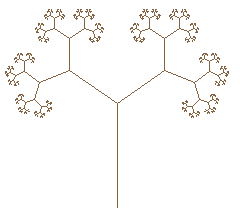
    if(keyPressed(SDLK_e) {enable1 = enable2 = enable3 = 1; enable4 = 0;a1 = a2 = a3 = 0; c1 = 0.5; c2 = 0.1; c3 = -0.7; size = h / 3; shrink = 1.5; maxRecursions = 8;} //a random tree with 3 branches
    if(keyPressed(SDLK_f) {enable1 = enable2 = enable3 = enable4 = 1; a1 = a2 = a3 = a4 = 0; c1 = 0.1 * pi; c2 = -0.1 * pi; c3 = 0.2 * pi; c4 = -0.2 * pi; size = h / 4; shrink = 1.25; maxRecursions = 6;} //a random tree with 4 branches
    if(keyPressed(SDLK_g) {enable1 = enable2 = enable3 = 1; enable4 = 0; a1 = 1; a2 = -1; a3 = 2.0; c1 = c2 = c3 = c4 = 0; size = h / 2; shrink = 2; maxRecursions = 6;} //some animating tree
    if(keyPressed(SDLK_h) {enable1 = enable2 = enable3 = 1; enable4 = 0; a1 = 1; a2 = -1; a3 = 2.5; c1 = c2 = c3 = c4 = 0; size = h / 2; shrink = 2; maxRecursions = 6;} //some animating tree
    if(keyPressed(SDLK_i) {enable1 = enable2 = enable3 = 1; enable4 = 0; a1 = 1; a2 = -1; a3 = 3.0; c1 = c2 = c3 = c4 = 0; size = h / 2; shrink = 2; maxRecursions = 6;} //some animating tree
    if(keyPressed(SDLK_SPACE)) {drawLeaves++; drawLeaves %= 5; releaseSpace = 0;}

  }
  return 0;
}

The recursion function is extended a bit too now:

First it'll clip and draw the line of the branch, and then, if the last recursion is reached, it'll draw a leave. Which type of leave it draws depends on the drawLeaves setting, that can be changed with the space key. If the max number of recursions is reached, the function returns so that it doesn't call itself anymore.

void recursionTree(double posX, double posY, double dirX, double dirY, double size, int n)
{
  int x1, x2, y1, y2;
  int x3, x4, y3, y4;
  x1 = int(posX);
  y1 = int(posY);
  x2 = int(posX + size * dirX);
  y2 = int(posY + size * dirY);
  if(clipLine(x1, y1, x2, y2, x3, y3, x4, y4))
  drawLine(x3, y3, x4, y4, ColorRGB(128, 96, 64));
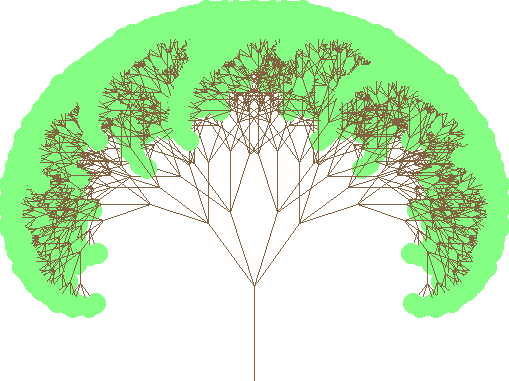
  if(n == maxRecursions && drawLeaves == 1) drawCircle(x4, y4, 5, ColorRGB(128, 255, 128));
  if(n == maxRecursions && drawLeaves == 2) drawDisk(x4, y4, 5, ColorRGB(128, 255, 128));
  if(n == maxRecursions && drawLeaves == 3) drawCircle(x4, y4, 10, ColorRGB(128, 255, 128));
  if(n == maxRecursions && drawLeaves == 4) drawDisk(x4, y4, 10, ColorRGB(128, 255, 128));

  if(n>=maxRecursions) return;

Finally, the function calculates new angles and vectors for the next branches and calls itself again, if that branch is enabled at least.

  double posX2, posY2, dirX2, dirY2, size2;
  int n2;
  posX2 = posX + size * dirX;
  posY2 = posY + size * dirY;
  size2 = size / shrink;
  n2 = n + 1;
  if(enable1)
  {
    dirX2 = cos(a1 * angle + c1) * dirX + sin(a1 * angle + c1) * dirY; //Rotation
    dirY2 = -sin(a1 * angle + c1) * dirX + cos(a1 * angle + c1) * dirY;
    recursionTree(posX2, posY2, dirX2, dirY2, size2, n2);
  }
  if(enable2)
  {
    dirX2 = cos(a2 * angle + c2) * dirX + sin(a2 * angle + c2) * dirY;
    dirY2 = -sin(a2 * angle + c2) * dirX + cos(a2 * angle + c2) * dirY;
    recursionTree(posX2, posY2, dirX2, dirY2, size2, n2);
  }
  if(enable3)
  {
    dirX2 = cos(a3 * angle + c3) * dirX + sin(a3 * angle + c3) * dirY;
    dirY2 = -sin(a3 * angle + c3) * dirX + cos(a3 * angle + c3) * dirY;
    recursionTree(posX2, posY2, dirX2, dirY2, size2, n2);
  }
  if(enable4)
  {
    dirX2 = cos(a4 * angle + c4) * dirX + sin(a4 * angle + c4) * dirY;
    dirY2 = -sin(a4 * angle + c4) * dirX + cos(a4 * angle + c4) * dirY;
    recursionTree(posX2, posY2, dirX2, dirY2, size2, n2);
  }
}

Here are just a few of the trees that can be generated this way:




You can do much more with this to create very natural trees, for example you can randomize the angle each recursion, or randomize whether or not a next branch will be drawn. You can draw thicker stems, with a texture, and nicer leaves instead, or even extend this to 3D and make some nice OpenGL demo! Use your fantasy :)
Last edited: 2004

Copyright (c) 2004-2007 by Lode Vandevenne. All rights reserved.