Lode's Computer Graphics Tutorial

Texture Generation using Random Noise

Introduction
Smooth Noise
Turbulence
Clouds
Marble
Wood
3D Random Noise

Introduction

In nature, everything has a random look, while mathematical formulas typically don't generate random looking results, unless you use them well. Random noise, such as Perlin noise invented by Ken Perlin, uses random numbers to generate natural looking textures.

Smooth Noise

As source for the random noise we need an array of random values, called noise[x][y]. Since our interest is generating 2D textures, a 2D array is used. The function generateNoise will fill the array with noise, and the main function is programmed to show this noise array on the screen. The noise itself is generated with the rand() function from the <cstdlib> header file, this function returns a random integer value between 0 and 32768 (as defined in the header file). It's normalized to a random real number between 0 and 1 by dividing it through 32768.0 (make sure to use floating point division).

#define noiseWidth 128
#define noiseHeight 128

double noise[noiseHeight][noiseWidth]; //the noise array

void generateNoise();

int main(int argc, char *argv[])
{
  screen(noiseWidth, noiseHeight, 0, "Random Noise");
  generateNoise();

  ColorRGB color;

  for(int y = 0; y < h; y++)
  for(int x = 0; x < w; x++)
  {
    color.r = color.g = color.b = Uint8(256 * noise[x][y]);
    pset(x, y, color);
  }

  redraw();
  sleep();
  return 0;
}

void generateNoise()
{
  for (int y = 0; y < noiseHeight; y++)
  for (int x = 0; x < noiseWidth; x++)
  {
    noise[y][x] = (rand() % 32768) / 32768.0;
  }
}

Here's the noise it generates:

This noise doesn't look very natural however, especially if you zoom in. Zoom in by dividing the x and y used to call the noise array through 8, in the pixel loop of the main function. You get something blocky:

    color.r = color.g = color.b = Uint8(256 * noise[y / 8][x / 8]);
    pset(x, y, color);

When zooming in, we want something smoother. For that, linear interpolation can be used. Currently the noise is an array and it's got only a discrete set of integer indices pointing to its contents. By using bilinear interpolation on the fractional part, you can make it smoother. For that, a new function, smoothNoise, is introduced:

double smoothNoise(double x, double y)
{
   //get fractional part of x and y
   double fractX = x - int(x);
   double fractY = y - int(y);

   //wrap around
   int x1 = (int(x) + noiseWidth) % noiseWidth;
   int y1 = (int(y) + noiseHeight) % noiseHeight;

   //neighbor values
   int x2 = (x1 + noiseWidth - 1) % noiseWidth;
   int y2 = (y1 + noiseHeight - 1) % noiseHeight;

   //smooth the noise with bilinear interpolation
   double value = 0.0;
   value += fractX     * fractY     * noise[y1][x1];
   value += (1 - fractX) * fractY     * noise[y1][x2];
   value += fractX     * (1 - fractY) * noise[y2][x1];
   value += (1 - fractX) * (1 - fractY) * noise[y2][x2];

   return value;
}

The returned value is the weighed average of 4 neighboring pixels of the array. In the main function, now use this instead of directly calling the noise array, and use real numbers for the division:

    color.r = color.g = color.b = Uint8(256 * smoothNoise(x / 8.0, y / 8.0));
    pset(x, y, color);

This is again the result zoomed in 8 times, but now with the bilinear interpolation. If you don't zoom in you won't be able to see the interpolation:

This is quite useful for random noise, the smoothing method could be better maybe, bilinear interpolation is often used by 3D cards for smoothing textures in games as a cheap and fast technique.

Let's call this image a "noise texture".

Turbulence

Turbulence is what creates natural looking features out of smoothed noise. The trick is to add multiple noise textures of different zooming scales together. An example of how this represents nature can be found in a mountain range: there are very large features (the main mountains), they are very deeply zoomed in noise.

Then added to the mountains are smaller features: multiple tops, variations in the slope, ...

Then, at an even smaller scale, there are rocks on the mountains.

An even smaller layer is the grains of sand. Together, the sum of all these layers forms natural looking mountains.

In 2D, this is done by adding different sizes of the smoothed noise together.

The zooming factor started at 16 here, and is divided through two each time. Keep doing this until the zooming factor is 1. The small features in the mountain example weren't only smaller in the width, but also in the height. To achieve this in 2D textures, make the images with a smaller zoom darker, so adding them will have less effect:

By adding these 5 images together, and dividing the result through 5 to get the average, you get a turbulence texture:

Here's a function that'll automaticly do all this for a single pixel. The parameter "size" is the initial zoom factor, which was 16 in the example above. The return value is normalized so that it'll be a number between 0 and 255.

double turbulence(double x, double y, double size)
{
  double value = 0.0, initialSize = size;

  while(size >= 1)
  {
    value += smoothNoise(x / size, y / size) * size;
    size /= 2.0;
  }

  return(128.0 * value / initialSize);
}

To use the turbulence function, change the small part of the code in the loop that goes through every pixel by the following:

    color.r = color.g = color.b = Uint8(turbulence(x, y, 64));
    pset(x, y, color);

The size is set to 64 there, and the result looks like this:

If you set the initial size to 256 instead, the result is much bigger and smoother:

And here's a very small initial size of only 8:

The textures here have some obvious horizontal and vertical lines because of the bilinear filter smooth function. The Clouds filter in Photoshop generates a texture similar to the ones above, but with a nicer smooth function. Nicer smooth functions are beyond the scope of this article though.

If you use no smooth function at all, it looks like this:

Clouds

To generate a sky with clouds, you can use the turbulence texture above, but with a blue-white color palette instead of black and white. For that the HSLtoRGB function can be used, with the hue set to blue (169 or 240°) and lightness ranging from 192 to 255 to make it white enough. Here's a new main function that'll do this:

#define noiseWidth 320
#define noiseHeight 240

double noise[noiseHeight][noiseWidth]; //the noise array

void generateNoise();
double smoothNoise(double x, double y);
double turbulence(double x, double y, double size);

int main(int argc, char *argv[])
{
  screen(noiseWidth, noiseHeight, 0, "Random Noise");
  generateNoise();

  Uint8 L;
  ColorRGB color;

  for(int y = 0; y < h; y++)
  for(int x = 0; x < w; x++)
  {
    L = 192 + Uint8(turbulence(x, y, 64)) / 4;
    color = HSLtoRGB(ColorHSL(169, 255, L));

    pset(x, y, color);
  }

  redraw();
  sleep();
  return 0;
}

Marble

It's possible to use random Noise to create a texture that looks like marble. To do this, a sine pattern is taken as base, a sine pattern looks like this:

The sine texture is generated by giving the pixel at position (x, y) the color value 255 * sin(x + y). You can change the angle and period (= amount of lines) by multiplying x and y with factors. The sine pattern has dark and bright lines, and by applying turbulence to these lines by adding a turbulence term in the sine, you get something that looks like the veins of marble:

int main(int argc, char *argv[])
{
  screen(noiseWidth, noiseHeight, 0, "Marble");
  generateNoise();

  ColorRGB color;

  //xPeriod and yPeriod together define the angle of the lines
  //xPeriod and yPeriod both 0 ==> it becomes a normal clouds or turbulence pattern
  double xPeriod = 5.0; //defines repetition of marble lines in x direction
  double yPeriod = 10.0; //defines repetition of marble lines in y direction
  //turbPower = 0 ==> it becomes a normal sine pattern
  double turbPower = 5.0; //makes twists
  double turbSize = 32.0; //initial size of the turbulence

  for(int y = 0; y < h; y++)
  for(int x = 0; x < w; x++)
  {
    double xyValue = x * xPeriod / noiseWidth + y * yPeriod / noiseHeight + turbPower * turbulence(x, y, turbSize) / 256.0;
    double sineValue = 256 * fabs(sin(xyValue * 3.14159));
    color.r = color.g = color.b = Uint8(sineValue);
    pset(x, y, color);
  }

  redraw();
  sleep();
  return 0;
}

The value "xyValue" is the sum of x multiplied with a factor, y multiplied with a factor, and the turbulence multiplied with a factor. xPeriod, yPeriod and turbPower are parameters that you can change to get different textures. The division through 256 of the turbulence is done to bring it to a value between 0 and 1, because the turbulence function was made to return values from 0 to 255. The values above give the following result:

Decreasing turbPower will give less twists, for example if you set it to 1.0, you get:

You can see much better how a sine pattern is used now, the dark and bright lines only twist a small bit, which still gives a sort of natural look.

Changing the initial size of the turbulence function makes the twists bigger (and thus much more subtle, similar to making turbPower smaller), while a small initial size gives much smaller but mor eaggressive twists. Here turbPower is set to 5.0 again, and turbSize to128.0 and 16.0 respectively:

Changing the period of x and y makes more or less black lines, for example here the lines are made wider and with an angle of 0° by setting xPeriod to 0 and yPeriod to 1 so that there'll be only one horizontal black line. turbSize is set to 32, and turbPower to only 1 so that you can see the direction of the line better:

Here are the same parameters, but turbPower back to 5, so you can see how a big enough turbulence really totally hides the fact that there's only one black line:

You can also change the colors of the marble by using a different value for R, G and B, for example to make it a bit red or yellowish:

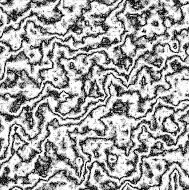
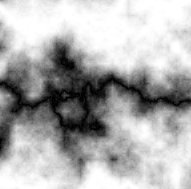
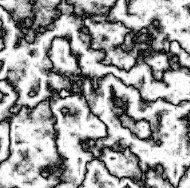
    double xyValue = x * xPeriod / noiseWidth + y * yPeriod / noiseHeight + turbPower * turbulence(x, y, turbSize) / 256.0;
    double sineValue = 226 * fabs(sin(xyValue * 3.14159));
    color.r = Uint8(30 + sineValue);
    color.g = Uint8(10 + sineValue);
    color.b = Uint8(sineValue);
    pset(x, y, color);

By playing around with the parameters you can get totally different marble or stone patterns.

Wood

Natural looking rings of wood can be created by adding turbulence to the following mathematical function:

To get the pattern above, take the sine of the distance of x and y to the center, so the color of the pixel at position x, y is 256 * sin(sqrt(x*x + y*y)). Add a turbulence term into the sine, and you get natural looking wood.

The values R, G and B are calculated out of the result in such a way that the wood will look brown:

int main(int argc, char *argv[])
{
  screen(noiseWidth, noiseHeight, 0, "Wood");
  generateNoise();

  ColorRGB color;

  double xyPeriod = 12.0; //number of rings
  double turbPower = 0.1; //makes twists
  double turbSize = 32.0; //initial size of the turbulence

  for(int y = 0; y < h; y++)
  for(int x = 0; x < w; x++)
  {
    double xValue = (x - noiseWidth / 2) / double(noiseWidth);
    double yValue = (y - noiseHeight / 2) / double(noiseHeight);
    double distValue = sqrt(xValue * xValue + yValue * yValue) + turbPower * turbulence(x, y, turbSize) / 256.0;
    double sineValue = 128.0 * fabs(sin(2 * xyPeriod * distValue * 3.14159));
    color.r = Uint8(80 + sineValue);
    color.g = Uint8(30 + sineValue);
    color.b = 30;
    pset(x, y, color);
  }

  redraw();
  sleep();
  return 0;
}

The rings are supposed to be visible here so, unlike for the marble, turbPower should be small.

Here's the result with more rings: xyPeriod is set to 25.

Here the wood has 12 rings again, but more turbulence: turbPower is set to 0.2:

If you make turbPower too high, the rings won't be visible anymore, and you'll get something that looks more like the marble patterns. Here it's set to 0.5:

So you see how you can turn a mathematical 2D function into a natural looking texture by adding noise to it. You can try this on much more functions, for example here's the mathematical pattern sin(x) + sin(y):

Add some noise to it with the following code:

    double xValue = (x - noiseWidth / 2) / double(noiseWidth) + turbPower * turbulence(x, y, turbSize) / 256.0;
    double yValue = (y - noiseHeight / 2) / double(noiseHeight) + turbPower * turbulence(h - y, w - x, turbSize) / 256.0;
    double sineValue = 22.0 * fabs(sin(xyPeriod * xValue * 3.1415) + sin(xyPeriod * yValue * 3.1415));
    color = HSVtoRGB(ColorHSV(Uint8(sineValue), 255, 255));
    pset(x, y, color);

And you get:

2D random noise can also be used for terrain heightmaps, physical simulations, etc...

3D Random Noise

Random Noise can be extended to any number of dimensions. The extension to 3D requires adding a z component, apart from a width and height the noise array now also needs a depth.

#define noiseWidth 192
#define noiseHeight 192
#define noiseDepth 64

double noise[noiseDepth][noiseHeight][noiseWidth]; //the noise array

The generateNoise function now needs to fill up the 3-dimensional array so it gets an extra loop:

void generateNoise()
{
  for(int z = 0; z < noiseDepth; z++)
  for(int y = 0; y < noiseHeight; y++)
  for(int x = 0; x < noiseWidth; x++)
  {
    noise[z][y][x] = (rand() % 32768) / 32768.0;
  }
}

The smoothing function now has to interpolate in the x, y and z direction so there are 8 terms instead of only 4:

double smoothNoise(double x, double y, double z)
{
  //get fractional part of x and y
  double fractX = x - int(x);
  double fractY = y - int(y);
  double fractZ = z - int(z);

  //wrap around
  int x1 = (int(x) + noiseWidth) % noiseWidth;
  int y1 = (int(y) + noiseHeight) % noiseHeight;
  int z1 = (int(z) + noiseDepth) % noiseDepth;

  //neighbor values
  int x2 = (x1 + noiseWidth - 1) % noiseWidth;
  int y2 = (y1 + noiseHeight - 1) % noiseHeight;
  int z2 = (z1 + noiseDepth - 1) % noiseDepth;

  //smooth the noise with bilinear interpolation
  double value = 0.0;
  value += fractX     * fractY     * fractZ     * noise[z1][y1][x1];
  value += fractX     * (1 - fractY) * fractZ     * noise[z1][y2][x1];
  value += (1 - fractX) * fractY     * fractZ     * noise[z1][y1][x2];
  value += (1 - fractX) * (1 - fractY) * fractZ     * noise[z1][y2][x2];

  value += fractX     * fractY     * (1 - fractZ) * noise[z2][y1][x1];
  value += fractX     * (1 - fractY) * (1 - fractZ) * noise[z2][y2][x1];
  value += (1 - fractX) * fractY     * (1 - fractZ) * noise[z2][y1][x2];
  value += (1 - fractX) * (1 - fractY) * (1 - fractZ) * noise[z2][y2][x2];

  return value;
}

The turbulence function is easy to extend, just add z / size to the call to the smoothNoise function:

double turbulence(double x, double y, double z, double size)
{
  double value = 0.0, initialSize = size;

  while(size >= 1)
  {
    value += smoothNoise(x / size, y / size, z / size) * size;
    size /= 2.0;
  }

  return(128.0 * value / initialSize);
}

The main function presented here will use the 3D random noise to generate clouds animated in the time. It's as if the clouds are forming and changing smoothly.

int main(int argc, char *argv[])
{
  screen(noiseWidth, noiseHeight, 0, "3D Random Noise");
  generateNoise();

  Uint8 L;
  ColorRGB color;
  double t;

  while(!done())
  {
    for(int y = 0; y < h; y++)
    for(int x = 0; x < w; x++)
    {
      L = 192 + Uint8(turbulence(x, y, t, 32)) / 4;
      color = HSLtoRGB(ColorHSL(169, 255, L));

      pset(x, y, color);

    }
    t = getTicks() / 40.0;
    redraw();
  }
  return 0;
}

The screenshot can't show how it animates of course:

3D andom noise can be used for animating 2D textures, for 3D textures (3D textures can for example be used on a rock of which you can remove parts or shoot pieces off it to see the inside of it, if you'd lay a 2D on it, and you remove a part of it, that same 2D texture would be drawn again), 3D planet textures, 3D volumetric fog, etc...