Lode's Computer Graphics Tutorial

Fourier Transform

Table of Contents

Back to Index

Introduction

The Fourier Transform is an important tool in Image Processing, and is directly related to filter theory, since a filter, which is a convolution in the spatial domain (=the image), is a simple multiplication in the spectral domain (= the FT of the image)!

Most other tutorials about Fourier Transforms of images are in boring greyscale. Even, many programs and plugins available that can calculate the FT on images only support greyscale. In times where 24 and 32 bit color are getting old, we cannot accept this any longer! This tutorial is in 24-bit color, by doing the FT on each colorchannel separately. Here's an example where the FT of an image is used to make a tillable grass texture look better:



There is also another way to calculate the FT of color images however, by using quaternions instead of complex numbers, which can convert an image of 4 channels to another image with 4 channels.

Before beginning with the Fourier Transform on images, which is the 2D version of the FT, we'll start with the easier 1D FT, which is often used for audio and electromagnetical signals.

To fully understand this tutorial, it'd be interesting to know about complex numbers, their magnitude (amplitude), and argument (phase). If you'd like to learn more about these, there's an appendix about complex numbers (one of the other html files), or find a tutorial with google.

The following two source files can be downloaded to have all the code described:

fourier2d.cpp
fourier1d.cpp

Libraries

This tutorial contains demo code for computing the Fourier Transform, however if you would like to use the Fourier Transform for any real application, there are better and faster libraries out there so I really recommend using those, and use the code in this tutorial only to follow along.

Specifically, the Fast Fourier Transform code further down in this tutorial only supports power-of-two sized inputs, while good libraries can do FFT on arbitrary sizes.

Here are a few good free libraries (carefully note which license they have to check if you can use it in your project):

Signals and Spectra

Before starting with the Fourier Transform, an introduction about Signals and Spectra is in place. As signals, for now consider signals in the time, like audio and electromagnetic signals. If you plot such a signal in function of time, a simple signal could look like this:



This is a sine wave, so if this'd be an audio signal, you'd hear a pure tone with only 1 frequency (like the beep of a PC speaker, or a very pure flute). The grey curve behind the red curve represents the amplitude of the signal, which is always positive.

The spectrum of a signal contains for every frequency, how much of this frequency is in the signal. Since the signal above is a sine, it has only one frequency, so the spectrum would be very simple: only one value will be positive (= the frequency of the sine curve), and all others are zero. So the spectrum would have a single peak. A spectrum has two sides however: the negative side on the left, and the positive side on the right. The negative side contains negative frequencies. For real signals (with no imaginary part), like audio signals are, the negative side of the spectrum is always a mirrored version of the positive side. So for the sine signal above, the positive side will have a single peak, and this peak will be mirrored in the negative side. This is what its spectrum looks like:



The white curve represents the amplitude of the signal. The red and green curve represent the real and imaginary part of the spectrum, respectively, but a spectrum is raraly represented that way. Normally, both the amplitude and phase of a spectrum are given, but since there's not that much interesting info for us in it now, the phase isn't included.

Let's study another example now: the same sine, but with a DC component added: sin(x)+C. The name DC component comes from electronics, where it stands for Direct Current (as opposed to Alternating Current). The DC component in any signal, is the time average of it. A sine signal has time average 0, but if however, you add a constant to the sine, the signals time average will become that constant. This adding of the constant, results in the sine signal being raised higher above the horizontal axis:



Such a constant, or DC component, has frequency 0. So we can expect that the spectrum will get an extra peak at the origin, and indeed, it has:



So, if the spectrum of a signal is non-zero at the origin, you know that its time average isn't zero and it has a DC component! The further away from the origin to the left or right a peak is, the higher the frequency it represents, so a peak far to the right (and left) means that the signal contains a high frequency component. Note that an audio signal never has a DC component, since nobody can produce or hear it. Electrical signals can have it however.

Now let's look at a signal which is the sum of two sine functions: the second sine function has the double frequency of the first, so the curve has the shape sin(x)+sin(2*x):



Since there are now two sines with two different frequencies, we can expect two peaks on the positive side of the spectrum (and two more on the negative side since it's the mirrored version):



If the two sines both have a different phase (i.e. one of the two sines is shifted horizontally), the amplitude of the spectum will still be the same, only the phase will be different, but the phase isn't shown here.

Arbitrary sound signals, such as a spoken word, consist of an infinite sum (or integral) of infinitely much sine functions, all with a different frequency, and all with their own amplitude and phase, and the spectrum is the perfect plot to view how much of each frequency is in the signal. Such a spectrum won't just have a few peaks, but will be a continuous function.

There are a few special functions with a special spectrum:

The Dirac impuls is a signal that is zero everywhere, except at the origin, where it's infinite. That is the ideal version for continuous functions, for a discrete function on a computer it can as well be represented as a single peak with finite height at the origin.



Such a peak sounds like a popping sound in an audio signal, and contains ALL frequencies. That's why its spectrum looks like this (the horizontal black line):



The spectrum is positive everywhere, so every frequency is contained in the signal. This also means that, to get such a peak as a sum of sine functions, you have to add infinitely much elementary sine functions all with the same amplitude, and all shifted with a certain phase, they'll cancel each other out, except at the origin, hence the peak.

Note that it's possible to intepret the spectrum as a time signal (a constant DC signal), and that then the red function can be seen as its spectrum (a peak at zero, since a DC signal has frequency 0). This duality is one of the interesting properties of the Fourier Transform as we'll see later.

Finally, another special signal is the sinc(x) function; sinc(x) = sin(x)/x:



Its spectrum is a rectangular pulse (here only an approximation of it because the spectrum was calculated using only 128 points):



Again because of the duality between a signal and its spectrum, a rectangular time signal will have a sinc function as its spectrum.

Spectra are also used to study the color of light. These are exactly the same thing, since light too is a 1-dimensional signal containing different frequencies, some of which the eye happens to be sensitive to. The spectrum shows for every frequency, how much of it is in the light, just the same as the audio spectrum does for audio signals.

An MP3 player like Winamp also shows the spectrum of the audio signal it's playing (but it varies with time because they calculate the spectrum each time again for the last few milliseconds), and spectra of audio signals can be used to detect bass, treble and vocals in music, for speach recognition, audio filters, etc... Since this is a tutorial about computer graphics, I won't go any deeper in this however.

Often, the spectrum is drawn on a logarithmical scale instead of a linear one like here, then the amplitude is expressed in decibels (dB).

The Fourier Transform

So how do you calculate the spectrum of a given signal? With the Fourier Transform!

The Continuous Fourier Transform, for use on continuous signals, is defined as follows:



And the Inverse Continuous Fourier Transform, which allows you to go from the spectrum back to the signal, is defined as:



F(w) is the spectrum, where w represents the frequency, and f(x) is the signal in the time where x represents the time. i is sqrt(-1), see complex number theory.

Note the similarity between both transforms, which explains the duality between a signal and its spectrum.

A computer can't work with continuous signals, only with finite discrete signals. Those are finite in time, and have only a discrete set of points (i.e. the signal is sampled). One of the properties of the Fourier Transform and its inverse is, that the FT of a discrete signal is periodic. Since for a computer both the signal and the specrum must be discrete, both the signal and spectrum will be periodic. But by taking only one period of it, we get our finite signal. So if you're taking the DFT of a signal or an image on the computer, mathematicaly speaking, that signal is infinitely repeated, or the image infinitely tiled, and so is the spectrum. A nice property is that both the signal and the spectrum will have the same number of discrete points, so the DFT of an image of 128*128 pixels will also have 128*128 pixels.

Since the signal is finite in time, the infinite borders of the integrals can be replaced by finite ones, and the integral symbol can be replaced by a sum. So the DFT is defined as:



And the inverse as:



This looks already much more programmable on a computer, to program the FT, you have to do the calculation for every n, so you get a double for loop (one for every n, and one for every k, which is the sum). The exponential of the imaginary number can be replaced by a cos and a sin by using the famous formula e^ix = cosx + isinx. More on programming it follows further in this tutorial.

There are multiple definitions of the DFT, for example you can also do the division through N in the forward DFT instead of the inverse one, or divide through sqrt(N) in both. To plot it on a computer, the best result is gotten by dividing through N in the forward DFT.

Properties of The Fourier Transform

A signal is often denoted with a small letter, and its fourier transform or spectrum with a capital letter. The relatoin between a signal and its spectrum is often denoted with f(x) <--> F(w), with the signal on the left and its spectrum on the right.

The Fourier Transform has some interesting properties, some of which make it easier to understand why spectra of certain signals have a certain shape.

Don't take this as a proper list however, some scaling factors like 2*pi are left away, they're not that important and can be left away or depending if you use frequency or pulsation. Handbooks of Sigal Processing and sites like Wikipedia and Mathworld contain much more complete and mathematically correct tables of FT properties. We're most interested in the shape of the functions and not the scale.

Linearity

f(x)+g(x) <--> F(w)+G(w)

a*f(x) <--> a*F(w)

This means that if you add/substract two signals, their spectra are added/substracted as wall, and if you increase/decrease the amplitude of the signal, the amplitude of its spectrum will be increased/decreased with the same factor.

Scaling

f(a*x) <--> (1/a) * F(w/a)

This means that if you make the function wider in the x-direction, its spectrum will become smaller in the x-direction, and vica versa. The amplitude will also be changed.

Time Shifting

f(x-x0) <--> (exp(-i*w*x0)) * F(w)

Since the only thing that happens if you shift the time, is a multiplication of the Fourier Transform with the exponential of an imaginary number, you won't see the difference of a time shift in the amplitude of the spectrum, only in the phase.

Frequency Shifting

(exp(-i*w0*x))*f(x)<-->F(w-w0)

This is the dual of the time shifting.

Duality or Symmetry

if f(x) <--> F(w)
then F(x) <--> f(-w)

Apart from some scaling factors at least. Because of this property, for example, the spectrum of a rectangular pulse is a sinc function and at the same time the spectrum of a sinc function is a rectangular pulse.

Symmetry Rules

These are only a few of the symmetry rules:

Convolution Theorem

Convolution is an operation between two functions that is defined as an integral, but can also be explained as follows:

Take 2 functions, for example two rectangle functions f1(x) and f2(x). Keep one of the rectangles at a fixed position. Mirror the second one around the y axis (this doesn't have a lot of effect on a rectangle). Then shift this second function over a value u, where u goes from -infinity to +infinity.

The resulting function g(u), the convolution of f1(x) and f2(x), takes u as a parameter. For a certain u, multiply f1 and the shifted and mirrored f2 with each other, and take area under the result (by integrating it). This area is the value of g(u) for that u! This has to be done for every u to know the complete result. For example, for the two rectangle functions, as we start at u=-infinity, g(u) is 0 because the two rectangles don't overlap, and multiplication of the two functions will thus result in the zero function, which has zero area. As u moves to the right, g(u) will remain 0 all the time, until finally the two rectangles start overlapping. Now the more we go to the right, the larger the area will become, until it reaches its maximum, so g(u) is rising. Then, the rectangles are overlapping less and less again as the second one moves more to the right, and the value of g(u) decreases again. Finally g(u) reaches zero again and remains so until +infinity. The resulting g(u) is thus a triangle function.

This is what filters of painting programs that don't use the FT do in 2D. The image is then the function that remains at fixed position, while the filter matrix moves around the whole image, and you calculate the value of every pixel by multiplying every element of the matrix with every corresponding pixel of the image the matrix overlaps. For large filter matrices this is a lot of work. You can create your own filter matrices in painting programs like Paint Shop Pro and Photoshop by using the "User Defined" filter.

Correlation is almost the same as convolution, except you don't have to mirror the second function.

The convolution theorem sais that, convolving two functions in the time domain corresponds to multiplying their spectra in the fourier domain, and vica versa. This multiplication is a much easier operation than convolution.

Since filters, too, can be described in the time and the fourier domain (called the impulse response and transfer function of the filter respectively), and linear filters do a convolutoin in the time domain, in the frequency domain this corresponds to multiplying the transfer function of the filter with the spectrum of the signal. The impulse response of the filter in the time domain is the response of the filter to a dirac impuls (see earlier), and the transfer function of the filter is the Fourier Transform of the impulse response.

For us, the Convolution Theorem will come in handy when we experiment with the Fourier Transformations of signals and images.

Programming The 1D Fourier Transform

Here's the code of a simple program that'll calculate the FT of a given signal, and will plot both the signal and the FT. Put it in the main.cpp file.

First the variables and functions are declared. N will be the number of discrete points in the signal. For the signal and its spectrum, respectively a small f or g and capital F or G are used, as it's also done in mathematics.

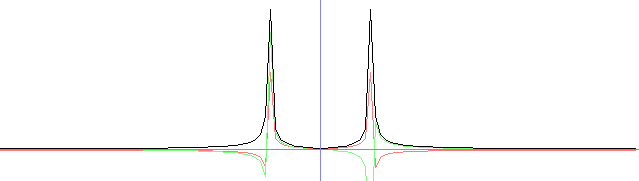
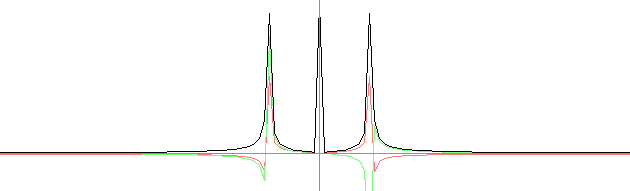
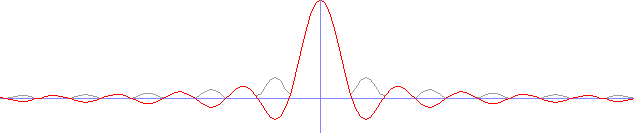
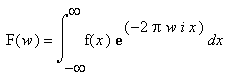
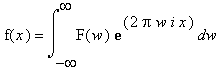
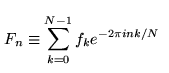
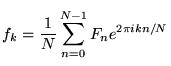
// working with fixed sizes for simplicity in this tutorial
const int N = 128;

double fRe[N]; //the function's real part, imaginary part, and amplitude
double fIm[N];
double fAmp[N];
double FRe[N]; //the FT's real part, imaginary part and amplitude
double FIm[N];
double FAmp[N];
const double pi = 3.1415926535897932384626433832795;

void DFT(int n, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm); //Calculates the DFT
void plot(int yPos, const double *g, double scale, bool trans, ColorRGB color); //plots a function
void calculateAmp(int n, double *ga, const double *gRe, const double *gIm); //calculates the amplitude of a complex function

The main function creates a sine signal, and will then use the other functions to calculate the FT and plot it.

int main(int /*argc*/, char */*argv*/[])
{
  screen(640, 480, 0, "1D DFT");
  cls(RGB_White);

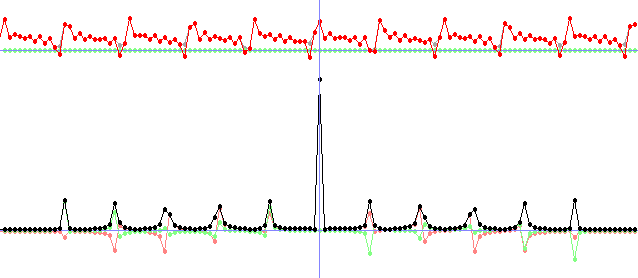
  for(int x = 0; x < N; x++)
  {
    fRe[x] = 25 * sin(x / 2.0); //generate a sine signal.  Put anything else you like here.
    fIm[x] = 0;
  }

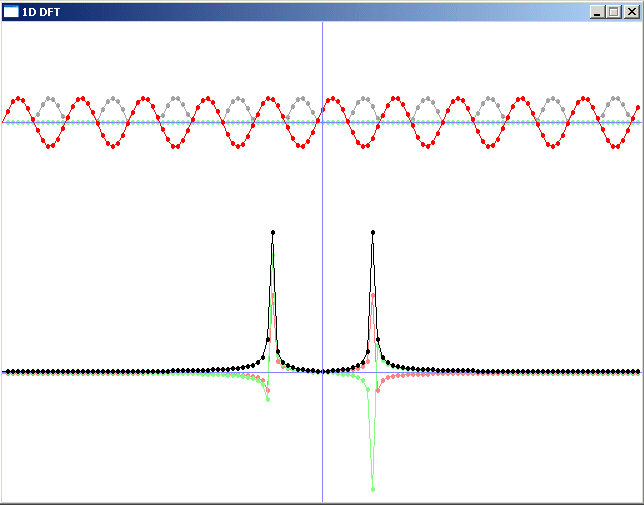
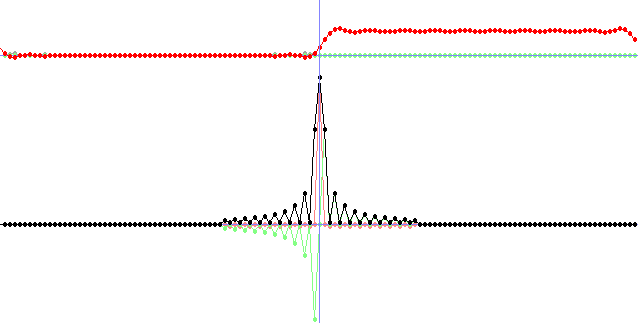
  //Plot the signal
  calculateAmp(N, fAmp, fRe, fIm);
  plot(100, fAmp, 1.0, 0, ColorRGB(160, 160, 160));
  plot(100, fIm, 1.0, 0, ColorRGB(128, 255, 128));
  plot(100, fRe, 1.0, 0, ColorRGB(255, 0, 0));

  DFT(N, 0, fRe, fIm, FRe, FIm);

  //Plot the FT of the signal
  calculateAmp(N, FAmp, FRe, FIm);
  plot(350, FRe, 12.0, 1, ColorRGB(255, 128, 128));
  plot(350, FIm, 12.0, 1, ColorRGB(128, 255, 128));
  plot(350, FAmp, 12.0, 1, ColorRGB(0, 0, 0));

  drawLine(w / 2, 0, w / 2, h - 1, ColorRGB(128, 128, 255));
  redraw();
  sleep();

  return 0;
}

Then comes the function that does the actual work (albeit with a very suboptimal algorithm here): the DFT function

void DFT(int n, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm)
{
  for(int w = 0; w < n; w++)
  {
    GRe[w] = GIm[w] = 0;
    for(int x = 0; x < n; x++)
    {
      double a = -2 * pi * w * x / float(n);
      if(inverse) a = -a;
      double ca = cos(a);
      double sa = sin(a);
      GRe[w] += gRe[x] * ca - gIm[x] * sa;
      GIm[w] += gRe[x] * sa + gIm[x] * ca;
    }
    if(!inverse)
    {
      GRe[w] /= n;
      GIm[w] /= n;
    }
  }
}

It takes 4 arrays as parameters: *gRe and *gIm to read from (these are the real and imaginary part of the signal), and *GRe and *GIm to write the results to (these are the FT of the signal). Both the input and output are complex numbers, which is why two arrays (a real and an imaginary one) are needed. n is the size of the signal (and the arrays), so it's the number of discrete points in the signal.

The first for loop with w going from 0 to n-1 means that a calculation is needed for every single point of the result. The second for loop, with x going from 0 to n, means that every point of the input signal needs to be taken in account, it's the sum from the mathematical definition of the DFT. The exponential function is changed by the formula e^ix = cosx + isinx, and the real and imaginary part are calculated seperatly. Afterwards the values are divided through n, so that the values are reasonably small enough to plot them on the screen.

By setting "inverse" to true, it can also calculate the IDFT (Inverse Discrete Fourier Transform), but this isn't used in this example. The only differences are a different sign in the exponential function and no division through n.

Next, the plot function takes a single array as parameter, and will draw the signal or spectrum contained in this array on screen with a color you want using lines and filled circles. You can also use a parameter "shift" to bring the edges to the center and vica versa. This is useful for a better representation of the Fourier Transform: normally the result of the DFT has the low frequency components on the sides, and the highest frequency in the center. Since the result is in fact periodic, bringing the sides to the center is the same as moving the plot half a period.

void plot(int yPos, const double *g, double scale, bool shift, ColorRGB color)
{
  drawLine(0, yPos, w - 1, yPos, ColorRGB(128, 128, 255));
  for(int x = 1; x < N; x++)
  {
    int x1, x2, y1, y2;
    int x3, x4, y3, y4;
    x1 = (x - 1) * 5;
    //Get first endpoint, use the one half a period away if shift is used
    if(!shift) y1 = -int(scale * g[x - 1]) + yPos;
    else y1 = -int(scale * g[(x - 1 + N / 2) % N]) + yPos;
    x2 = x * 5;
    //Get next endpoint, use the one half a period away if shift is used
    if(!shift) y2 = -int(scale * g[x]) + yPos;
    else y2 = -int(scale * g[(x + N / 2) % N]) + yPos;
    //Clip the line to the screen so we won't be drawing outside the screen
    clipLine(x1, y1, x2, y2, x3, y3, x4, y4);
    drawLine(x3, y3, x4, y4, color);
    //Draw circles to show that our function is made out of discrete points
    drawDisk(x4, y4, 2, color);
  }
}

And finally, the function calculateAmp calculates the amplitude given the real and imaginary part, so you can plot the amplitude too.

//Calculates the amplitude of *gRe and *gIm and puts the result in *gAmp
void calculateAmp(int n, double *gAmp, const double *gRe, const double *gIm)
{
  for(int x = 0; x < n; x++)
  {
    gAmp[x] = sqrt(gRe[x] * gRe[x] + gIm[x] * gIm[x]);
  }
}

The output of this program is as follows:



The red function is the input function, which is a sine, and the black funtion at the bottom is the amplitude of its spectrum, which is calculated by the DFT function. The green curves are the imaginary parts.

The Fast Fourier Transform

The above DFT function correctly calculates the Discrete Fourier Transform, but uses two for loops of n times, so it takes O(n²) arithmetical operations. A faster algorithm is the Fast Fourier Transform or FFT, which uses only O(n*logn) operations. This makes a big difference for very large n: if n would be 1024, the DFT function would take 1048576 (about 1 million) loops, while the FFT would use only 10240.

The FFT works by splitting the signal into two halves: one halve contains all the values with even index, the other all the ones with odd index. Then, it splits up these two halves again, etc..., recursivily. Due to this, a requirement is that the size of the signal, n, must be a power of 2. The algorithm described here is the Radix-2 Cooley-Tukey FFT algorithm (developed by Cooley and Tukey in 1965).

There exist other algorithms that can operate fast on signals with other sizes than a power of two, even large primes. For example mixed-radix Cooley-Tukey as well as others. However, this is beyond the scope of this tutorial. The code linked to in the Libraries section above supports non-powers of two so I would recommend using a library like those for real life applications. But for this tutorial, we continue with much simpler code for the demonstration.

Here's a new version of the DFT function, called FFT, which uses the radix-2 algorithm described above. You can add it to the previous program and change the function call of it to FFT to test it out.

First, this function will calculate the logarithm of n, needed for the algorithm.

void FFT(int n, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm)
{
  //Calculate m=log_2(n)
  int m = 0;
  int p = 1;
  while(p < n)
  {
    p *= 2;
    m++;
  }

Next, Bit Reversal is performed. Because of the way the FFT works, by splitting the signal in its even and odd components every time, the algorithm requires that the input signal is already in the form where all odd components come first, then the even ones, and so on in each of the halves. This is the same as reversing the bits of the index of each value (for example the second value, with index 0001 will now get index 1000 and this go to the center), hence the name.

  //Bit reversal
  GRe[n - 1] = gRe[n - 1];
  GIm[n - 1] = gIm[n - 1];
  int j = 0;
  for(int i = 0; i < n - 1; i++)
  {
    GRe[i] = gRe[j];
    GIm[i] = gIm[j];
    int k = n / 2;
    while(k <= j)
    {
      j -= k;
      k /= 2;
    }
    j += k;
  }

Next the actual FFT is performed. Mathematically speaking it's a recursive function, but this is a modified version to work non-recursively, it'd be way too hard to pass complete arrays to a recursive function every time. ca and sa still represent the cosine and sine, but are calculated with the half-angle formulas and initual values -1.0 and 0.0 (cos and sin of pi): each loop, ca and sa represent the cosine and sine of half the angle as the previous loop.

  //Calculate the FFT
  double ca = -1.0;
  double sa = 0.0;
  int l1 = 1, l2 = 1;
  for(int l = 0; l < m; l++)
  {
    l1 = l2;
    l2 *= 2;
    double u1 = 1.0;
    double u2 = 0.0;
    for(int j = 0; j < l1; j++)
    {
      for(int i = j; i < n; i += l2)
      {
        int i1 = i + l1;
        double t1 = u1 * GRe[i1] - u2 * GIm[i1];
        double t2 = u1 * GIm[i1] + u2 * GRe[i1];
        GRe[i1] = GRe[i] - t1;
        GIm[i1] = GIm[i] - t2;
        GRe[i] += t1;
        GIm[i] += t2;
      }
      double z =  u1 * ca - u2 * sa;
      u2 = u1 * sa + u2 * ca;
      u1 = z;
    }
    sa = sqrt((1.0 - ca) / 2.0);
    if(!inverse) sa =- sa;
    ca = sqrt((1.0 + ca) / 2.0);
  }

Finally, the values are divided through n if it isn't the inverse DFT.

  //Divide through n if it isn't the IDFT
  if(!inverse)
  for(int i = 0; i < n; i++)
  {
    GRe[i] /= n;
    GIm[i] /= n;
  }
}

The function reads from *gRe and *gIm again and stores the result in *GRe and *GIm.

There are 3 nested loops now in the FFT part, but only the first one goes from 0 to n-1, the other two together only loop log_2(n) times. For this small signal of only 128 values you probably won't notice any increase in speed because both DFT and FFT are calculated instantly (unless you're working on some computer from the '40s), but on bigger signals, on 2D signals, and in applications where the FT has be be calculated over and over in real time, it'll make an important difference.

Filters

In the Fourier Domain, it's easy to apply some filters. All you have to do is multiply the spectrum with the transfer function of the filter.

Low pass filters only let through components with low frequencies (for example the bass from music), while High Pass filters let only components with high frequencies through. You can also make Band Pass and Band Stop filters, which let through or block components with a certain frequency. Amplifiers multiply the whole spectrum with a constant value, and you can of course make filters that amplify certain frequencies, or triangular filters that weaken higher frequencies more and more, etc...

So to make for example a Low Pass filter, multiply the spectrum with a rectangular function with the rectangle around the origin. All the low frequency components will then be kept, while the high ones are multiplied by zero and are thus filtered away.

Here's a part of code for a program that'll first allow you to select different signals and watch their FT, and after pressing the space key, will allow you to choose different filters on the spectrum, and it'll calculate the inverse FT to see how the original signal is affected by the filter.

The full code can be downloaded here: fourier1d.cpp.

First all variables and functions are declared.

const int N = 128; //yeah ok, we use old fashioned fixed size arrays here

double fRe[N]; //the function's real part, imaginary part, and amplitude
double fIm[N];
double fAmp[N];
double FRe[N]; //the FT's real part, imaginary part and amplitude
double FIm[N];
double FAmp[N];
const double pi = 3.1415926535897932384626433832795;

void FFT(int n, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm); //Calculates the DFT
void plot(int yPos, const double *g, double scale, bool trans, ColorRGB color); //plots a function
void calculateAmp(int n, double *ga, const double *gRe, const double *gIm); //calculates the amplitude of a complex function

The main function starts here. It enters the first loop, this loop will allow you to choose a function. The parameters p1 and p2 can be changed to modify the amplitude and/or width of some of the functions.

int main(int /*argc*/, char */*argv*/[])
{
  screen(640, 480, 0, "Fourier Transform and Filters");
  for(int x = 0; x < N; x++) fRe[x] = fIm[x] = 0;
  bool endloop = 0, changed = 1;
  int n = N;
  double p1 = 25.0, p2 = 2.0;
  while(!endloop)
  {
    if(done()) end();
    readKeys();

This is inside the loop after it has read the keys. Every key has another action assiciated to it to create a certain function, for example if you press the g key (SDLK_g) it'll put a sum of two sines in fRe[x]. The arrow keys also have some actions to set the imaginary part to 0, equal to the real part, or a modified version of the real part. Finally, the space keys sets "endloop" to true so that the first loop will end.

Not all keys are included here, because it's very messy and big code. Only a few are shown as an example, the rest is in the downloadable source file.

    if(keyPressed(SDLK_z)) {for(int x = 0; x < n; x++) fRe[x] = 0; changed = 1;} //zero
    if(keyPressed(SDLK_a)) {for(int x = 0; x < n; x++) fRe[x] = p1; changed = 1;} //constant
    if(keyPressed(SDLK_b)) {for(int x = 0; x < n; x++) fRe[x] = p1 * sin(x / p2); changed = 1;} //sine


    //ETCETERA... *snip*

    if(keyPressed(SDLK_SPACE)) endloop = 1;

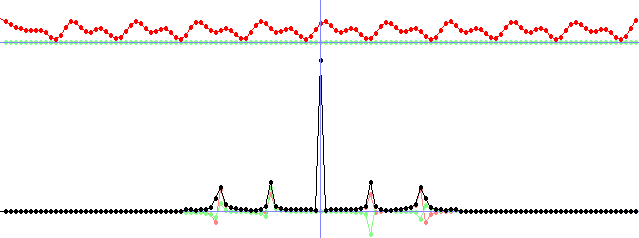
This is the last part of the first loop, where it draws the chosen function, calculates its FT, and draws that one too.

    if(changed)
    {
      cls(RGB_White);
      calculateAmp(N, fAmp, fRe, fIm);
      plot(100, fAmp, 1.0, 0, ColorRGB(160, 160, 160));
      plot(100, fIm, 1.0, 0, ColorRGB(128, 255, 128));
      plot(100, fRe, 1.0, 0, ColorRGB(255, 0, 0));

      FFT(N, 0, fRe, fIm, FRe, FIm);
      calculateAmp(N, FAmp, FRe, FIm);
      plot(350, FRe, 12.0, 1, ColorRGB(255, 128, 128));
      plot(350, FIm, 12.0, 1, ColorRGB(128, 255, 128));
      plot(350, FAmp, 12.0, 1, ColorRGB(0, 0, 0));

      drawLine(w / 2, 0, w / 2, h - 1, ColorRGB(128, 128, 255));
      print("Press a-z to choose a function, press the arrows to change the imaginary part, press space to accept.", 0, 0, RGB_Black);
      redraw();
    }
    changed = 0;
  }

After the first loop has ended, the second part of the main function starts. First, an extra spectrum buffer is created, so that both the original spectrum and its filtered version can be remembered. Then the second loop starts.

  //The original FRe2, FIm2 and FAmp2 will become multiplied by the filter
  double FRe2[N];
  double FIm2[N];
  double FAmp2[N];
  for(int x = 0; x < N; x++)
  {
    FRe2[x] = FRe[x];
    FIm2[x] = FIm[x];
  }
  cls();
  changed = 1; endloop = 0;
  while(!endloop)
  {
    if(done()) end();
    readKeys();

Now the keys all change the spectrum in a certain way: they'll aplly a filter. Low Pass filters (LP) set the spectrum to 0, except around the origin. High Pass filters (HP) do the oposite.

Not all keys are shown here, because it's very messy and big code. Only a few are shown as an example, the rest is in the downloadable source file in a more closely packed form.


    if(keyPressed(SDLK_z))
    {
      for(int x = 0; x < n; x++)
      {
        FRe2[x] = FRe[x];
        FIm2[x] = FIm[x];
      }
      changed = 1;
    } //no filter
    if(keyPressed(SDLK_a))
    {
      for(int x = 0; x < n; x++)
      {
        if(x < 44 || x > N - 44)
        {
          FRe2[x] = FRe[x];
          FIm2[x] = FIm[x];
        }
        else FRe2[x] = FIm2[x] = 0;
      }
      changed = 1;
    } //LP

    //ETCETERA... *snip*

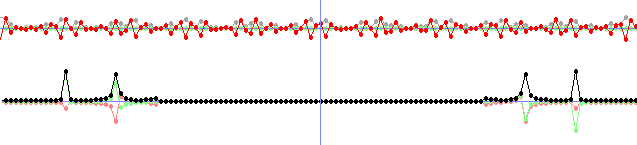
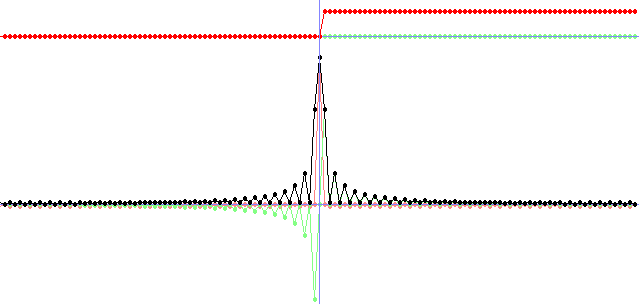
Again, if a key was pressed, the new spectrum is drawn, and the inverse FFT is performed to draw the filtered version of the original function. If you press escape the program will end.


    if(changed)
    {
      cls(RGB_White);
      FFT(N, 1, FRe2, FIm2, fRe, fIm);
      calculateAmp(N, fAmp, fRe, fIm);
      plot(100, fAmp, 1.0, 0, ColorRGB(160, 160, 160));
      plot(100, fIm, 1.0, 0, ColorRGB(128, 255, 128));
      plot(100, fRe, 1.0, 0, ColorRGB(255, 0, 0));

      calculateAmp(N, FAmp2, FRe2, FIm2);

      plot(350, FRe2, 12.0, 1, ColorRGB(255, 128, 128));
      plot(350, FIm2, 12.0, 1, ColorRGB(128, 255, 128));
      plot(350, FAmp2, 12.0, 1, ColorRGB(0, 0, 0));

      drawLine(w/2, 0,w/2,h-1, ColorRGB(128, 128, 255));
      print("Press a-z to choose a filter. Press esc to quit.", 0, 0, RGB_Black);
      redraw();
    }
    changed=0;
  }

  return 0;
}

The functions FFT, plot and calculateAmp are identical to the ones explained earlier and aren't included here anymore.

There's not much new in this code, the functions FFT, plot and calculateAmp are still the same, but by playing with this program you can see the effects of Low Pass (LP), High Pass (HP) and a few other filters. Just follow the instructions on screen.

For example, here, a signal which is the sum of 5 sines and a DC component (gotten by pressing the "p" key) is shown together with its spectrum, and then, respectively, a LP and a HP are applied to it:

The original signal:


An LP Filter:


A HP Filter

Here, the same is done with a step function (gotten by pressing the "e" key):


An LP filter on it:



A HP filter on it. This filter filters out almost only the DC component, so two almost-flat lines remain in the signal:



2D Fourier Transform on Images

The extension of the Fourier Transform to 2D is actually pretty simple. First you take the 1D FT of every row of the image, and then on this result you take the 1D FT of every column.

This can be done by doing FT row by row on the image with the 1D FT function, then transpose the image (so what were columns are now rows), then do again the 1D FT on each row, and then transpose the image again to have the original direction. This has the advantage the memory you're operating on is closer together for better caching for the CPU (faster), but requires a transpose operation in between. Another way is to extend the 1D FT function to take a "stride" parameter, which is the step in memory between successive values we're currently working on. The stride is then set to the row size to work on a column, or to 1 to work on rows. In addition, because we have 3 color channels, we multiply the stride by 3. This is slightly simpler so we'll use this method in this tutorial.


Here follows the code of a program that does exactly that, and two alternative functions that do the same are given in it: one will use the 2D version of the slow DFT, and the other the 2D version of the Fast Fourier Transform (FFT). The program will first calculate the FT of the image, and then calculate the Inverse FT of the result, to check if the formula is working correctly: if it gives back the original it works. You can freely change between calls to DFT2D() and FFT2D() in the main function, and you'll notice that the DFT2D() function is very slow now, while the FFT2D() function works very fast.

Because an RGB image has 3 color channels, the FT is calculated for each color channel separately, so in fact 3 greyscale FT's are calculated.

The program requires that there's a 24-bit color, 128*128 PNG image pics/test.png (path relative to the program). There is one in photos.zip
.
First again all the variables and functions are declared.
W and H are the width and height of the image in pixels.
The arrays for the signal and its spectrum are now 3-dimensional: 2 dimensions for the size, and 1 dimension for the RGB color components. The class ColorRGB can't be used here because more precision is required for FT, that's why the color components are put in a double array instead; index 0 represents red, index 1 green, and index 2 is blue.

There are two versions of the FT functions here, the slow DFT2D and the fast FFT2D.

/// working with fixed sizes for simplicity in this tutorial
const int W = 128; //the width of the image
const int H = 128; //the height of the image

double fRe[H][W][3], fIm[H][W][3], fAmp[H][W][3]; //the signal's real part, imaginary part, and amplitude
double FRe[H][W][3], FIm[H][W][3], FAmp[H][W][3]; //the FT's real part, imaginary part and amplitude
double fRe2[H][W][3], fIm2[H][W][3], fAmp2[H][W][3]; //will become the signal again after IDFT of the spectrum
double FRe2[H][W][3], FIm2[H][W][3], FAmp2[H][W][3]; //filtered spectrum

double pi = 3.1415926535897932384626433832795;

void draw(int xpos, int yPos, int w, int h, const double *g, bool shift, bool neg128);
void DFT2D(int w, int h, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm);
void FFT2D(int w, int h, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm);
void calculateAmp(int w, int h, double *ga, const double *gRe, const double *gIm);

The main function first loads an image, and then sets the signal to that image.

Next, it draws the image. It draws the real part, the imaginary part (which is 0!), and the amplitude, which looks the same as the real part.

Then it calculates the FT of the image, by using the DFT2D function, but you can as well change this to FFT2D instead: it'll go faster then. Then it draws the just calculated spectrum.

Finally, it calculates the inverse FT of that spectrum again and draws the result, this is only to check if the functions are working correctly: if you get the original image back, they are.

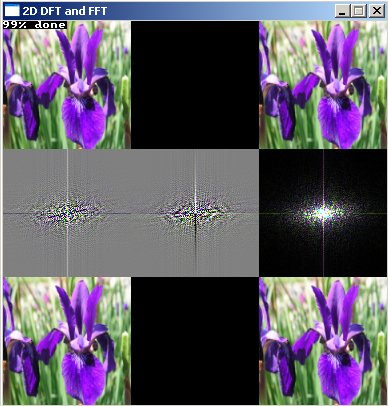
int main(int /*argc*/, char */*argv*/[])
{
  screen(N * 3, M * 3, 0, "2D DFT and FFT");

  std::vector<ColorRGB> img;
  unsigned long dummyw, dummyh;
  if(loadImage(img, dummyw, dummyh, "pics/test.png"))
  {
    print("image pics/test.png not found");
    redraw();
    sleep();
    cls();
  }

  //set signal to the image
  for(int y = 0; y < H; y++)
  for(int x = 0; x < W; x++)
  {
    fRe[y][x][0] = img[W * y + x].r;
    fRe[y][x][1] = img[W * y + x].g;
    fRe[y][x][2] = img[W * y + x].b;
  }

  //draw the image (real, imaginary and amplitude)
  calculateAmp(W, H, fAmp[0][0], fRe[0][0], fIm[0][0]);
  draw(0, 0, W, H, fRe[0][0], 0, 0);
  draw(W, 0, W, H, fIm[0][0], 0, 0);
  draw(2 * W, 0, W, H, fAmp[0][0], 0, 0);

  //calculate and draw the FT of the image
  DFT2D(W, H, 0, fRe[0][0], fIm[0][0], FRe[0][0], FIm[0][0]); //Change this to FFT2D to make it faster
  calculateAmp(W, H, FAmp[0][0], FRe[0][0], FIm[0][0]);
  draw(0, H, W, H, FRe[0][0], 1, 1);
  draw(W, H, W, H, FIm[0][0], 1, 1);
  draw(2 * W, H, W, H, FAmp[0][0], 1, 0);

  //calculate and draw the image again
  DFT2D(W, H, 1, FRe[0][0], FIm[0][0], fRe2[0][0], fIm2[0][0]); //Change this to FFT2D to make it faster
  calculateAmp(W, H, fAmp2[0][0], fRe2[0][0], fIm2[0][0]);
  draw(0, 2 * H, W, H, fRe2[0][0], 0, 0);
  draw(W, 2 * H, W, H, fIm2[0][0], 0, 0);
  draw(2 * W, 2 * H, W, H, fAmp2[0][0], 0, 0);

  redraw();
  sleep();
  return 0;
}

Here we have the 1D DFT function again, but this time with a stride and factor parameter added. The stride parameter, as explained above, allows a larger step, to allow working on columns and color channels in our 3D array. The factor is there because we need control over what values (rather than just n) to divide the result with.

void DFT(int n, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm, int stride, double factor)
{
  for(int n = 0; n < n; n++)
  {
    GRe[n * stride] = GIm[n * stride] = 0;
    for(int x = 0; x < n; x++)
    {
      double a = -2 * pi * n * x / float(n);
      if(inverse) a = -a;
      double ca = cos(a);
      double sa = sin(a);
      GRe[n * stride] += gRe[x * stride] * ca - gIm[x * stride] * sa;
      GIm[n * stride] += gRe[x * stride] * sa + gIm[x * stride] * ca;
    }
    //Divide through the factor, e.g. n
    GRe[n * stride] /= factor;
    GIm[n * stride] /= factor;
  }
}

The DFT2D function, then, calls the 2D DFT function for each row, and for each column, and this separately for every color component. The function takes now two parameters for the dimensions: w and h (sometimes also called n and m), because an image is 2D. The parameter inverse can be set to true to do the inverse calculations instead. Again *gRe and *gIm are the input arrays, and *GRe and *GIm the output arrays. In this 2D version, the values are divided through h for the normal DFT and through w for the inverse DFT. There are also definitions where you should divide through h*w in one direction and through 1 in the other, or though sqrt(h*w) in both, but it doesn't really matter which one you pick, as long as the forward FT and the inverse together give the original image back. Using roughly the square root of h*w in each direction, though, gives a similar range of values as the input image so is nicest to draw.

void DFT2D(int w, int h, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm)
{
  //temporary buffers
  std::vector<double> Gr2(m * n * 3);
  std::vector<double> Gi2(m * n * 3);

  for(int y = 0; y < h; y++) // for each row
  for(int c = 0; c < 3; c++) // for each color channel
  {
    DFT(w, inverse, &gRe[y * w * 3 + c], &gIm[y * w * 3 + c], &Gr2[y * w * 3 + c], &Gi2[y * w * 3 + c], 3, 1);
  }
  for(int x = 0; x < w; x++) // for each column
  for(int c = 0; c < 3; c++) // for each color channel
  {
    DFT(h, inverse, &Gr2[x * 3 + c], &Gi2[x * 3 + c], &GRe[x * 3 + c], &GIm[x * 3 + c], w * 3, inverse ? w : h);
  }
}

And here's the Fast Fourier Transform again, with stride and factor now.

void FFT(int n, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm, int stride, double factor)
{
  //Calculate h=log_2(n)
  int h = 0;
  int p = 1;
  while(p < n)
  {
    p *= 2;
    h++;
  }
  //Bit reversal
  GRe[(n - 1) * stride] = gRe[(n - 1) * stride];
  GIm[(n - 1) * stride] = gIm[(n - 1) * stride];
  int j = 0;
  for(int i = 0; i < n - 1; i++)
  {
    GRe[i * stride] = gRe[j * stride];
    GIm[i * stride] = gIm[j * stride];
    int k = n / 2;
    while(k <= j)
    {
      j -= k;
      k /= 2;
    }
    j += k;
  }
  //Calculate the FFT
  double ca = -1.0;
  double sa = 0.0;
  int l1 = 1, l2 = 1;
  for(int l = 0; l < h; l++)
  {
    l1 = l2;
    l2 *= 2;
    double u1 = 1.0;
    double u2 = 0.0;
    for(int j = 0; j < l1; j++)
    {
      for(int i = j; i < n; i += l2)
      {
        int i1 = i + l1;
        double t1 = u1 * GRe[i1 * stride] - u2 * GIm[i1 * stride];
        double t2 = u1 * GIm[i1 * stride] + u2 * GRe[i1 * stride];
        GRe[i1 * stride] = GRe[i * stride] - t1;
        GIm[i1 * stride] = GIm[i * stride] - t2;
        GRe[i * stride] += t1;
        GIm[i * stride] += t2;
      }
      double z =  u1 * ca - u2 * sa;
      u2 = u1 * sa + u2 * ca;
      u1 = z;
    }
    sa = sqrt((1.0 - ca) / 2.0);
    if(!inverse) sa =- sa;
    ca = sqrt((1.0 + ca) / 2.0);
  }
  //Divide through the factor, e.g. n
  for(int i = 0; i < n; i++)
  {
    GRe[i * stride] /= factor;
    GIm[i * stride] /= factor;
  }
}

Making it 2D is exactly the same as for DFT2D, but with the FFT function

void FFT2D(int w, int h, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm)
{
  //temporary buffers
  std::vector<double> Gr2(m * n * 3);
  std::vector<double> Gi2(m * n * 3);

  for(int y = 0; y < h; y++) // for each row
  for(int c = 0; c < 3; c++) // for each color channel
  {
    FFT(w, inverse, &gRe[y * w * 3 + c], &gIm[y * w * 3 + c], &Gr2[y * w * 3 + c], &Gi2[y * w * 3 + c], 3, 1);
  }
  for(int x = 0; x < w; x++) // for each column
  for(int c = 0; c < 3; c++) // for each color channel
  {
    FFT(h, inverse, &Gr2[x * 3 + c], &Gi2[x * 3 + c], &GRe[x * 3 + c], &GIm[x * 3 + c], w * 3, inverse ? w : h);
  }
}

The draw function does what the plot function did in the 1D version: show the signal on screen. Now this function will draw the signal or spectrum arrays you feed it as a 24-bit RGB image with the upper left corner at xpos,yPos. The shift parameter can be used to bring the corners to the center and the center to the corners, useful for FT's to bring the DC component to the center. The neg128 parameter can be used to draw images that can have negative pixel values: now gray (RGB color 128, 128, 128) is used as 0, darker colors are negative, and brighter ones are positive.

//Draws an image
void draw(int xPos, int yPos, int n, int m, const double *g, bool shift, bool neg128) //g is the image to be drawn
{
  for(int y = 0; y < m; y++)
  for(int x = 0; x < n; x++)
  {
    int x2 = x, y2 = y;
    if(shift) {x2 = (x + n / 2) % n; y2 = (y + m / 2) % m;} //Shift corners to center
    ColorRGB color;
    //calculate color values out of the floating point buffer
    color.r = int(g[3 * w * y2 + 3 * x2 + 0]);
    color.g = int(g[3 * w * y2 + 3 * x2 + 1]);
    color.b = int(g[3 * w * y2 + 3 * x2 + 2]);

    if(neg128) color = color + RGB_Gray;
    //negative colors give confusing effects so set them to 0
    if(color.r < 0) color.r = 0;
    if(color.g < 0) color.g = 0;
    if(color.b < 0) color.b = 0;
    //set color components higher than 255 to 255
    if(color.r > 255) color.r = 255;
    if(color.g > 255) color.g = 255;
    if(color.b > 255) color.b = 255;
    //plot the pixel
    pset(x + xPos, y + yPos, color);
  }
}

The calculateAmp function is also again the same as the 1D version, only with an extra loop for the 2nd dimension, and another one for the color components. This function is used to generate the amplitudes of the signals and spectra so that you can draw those.

//Calculates the amplitude of *gRe and *gIm and puts the result in *gAmp
void calculateAmp(int n, int m, double *gAmp, const double *gRe, const double *gIm)
{
  for(int y = 0; y < m; y++)
  for(int x = 0; x < n; x++)
  for(int c = 0; c < 3; c++)
  {
    gAmp[w * 3 * y + 3 * x + c] = sqrt(gRe[w * 3 * y + 3 * x + c] * gRe[w * 3 * y + 3 * x + c] + gIm[w * 3 * y + 3 * x + c] * gIm[w * 3 * y + 3 * x + c]);
  }
}

Note that, because of the way C++ works, the arrays are passed to the functions in a special way, and inside the functions they have to be treated as 1-dimensional.


Please note that above code is not at all optimal but kept simple for demonstration. Much faster libraries exist to do this, such as FFTW, kissfft and others. These are much faster, more complete, and support non-power-of-two sizes fast as well. Using such a well tested fast implementation is recommended for real life problems.

The output of the program is as follows:

2D DFT

On the top row are the real part, imaginary part and amplitude of the image. The imaginary part of the image is 0.

On the center row are the real part, imaginary part and amplitude of the spectrum from the image. The real and imaginary part can have negative values, so they have the "neg128" option enabled to draw them and grey represents 0. Since the amplitude is always positive, black is 0 there.

The bottom row is again the image, calculated by using the Inverse DFT of the spectrum. It looks almost the same as the original, a few pixels might slightly differ in color due to rounding errors.

The text "99% done" only appears if you use the DFT2D function, since it's so slow (30 seconds on an Athlon 1700+ processor for an 128x128 image) a progress counter is handy. The FFT2D does the same calculation immediatly, so such a counter isn't needed.

If you study the spectra of the images, you'll see horizontal and vertical lines through the center. They're caused by the sides of the image: since mathematically speaking, the FT is calculated of the image tiled infinite times, there's an abrupt change when going from one side of the image to the other, causing the lines in the spectrum.

Some remarks:

The Spectra of Images

You can replace test.png by any 24-bit 128*128 color PNG you want. You can even use another size, but then you'll have to change the parameters N and M in the code (on top). Note that the FFT2D function only works on images with a size that is a power of two (64x64, 128x256, 256x256... all work), otherwise you'll have to use the slower DFT2D function (or a good other FFT library that supports non power of two).

The spectrum of an image isn't immediatly the most interesting thing (applying filters on it and then taking the inverse FT again is much more interesting), but you can still learn a bit about an image by looking at its spectrum: here are a few examples, each picture shows the real part of the image, and the amplitude of the spectrum. To see the real and imaginary part of the spectrum, run the images through the program yourself.

This image is a sine function with a DC component added (because images can only have positive pixel values): the color of each pixel is 128 + 128 * sin(pi*y/16.0). If you remember the spectra of 1D signals, you'll remember that a sine function gave a peak on the negative and positive side, and that the DC component gave a peak at zero. Here you can see the same in the spectrum: the center dot is the DC component, and the two others represent the frequency of the sine function, the one dot is just a mirrored version of the other one. There are no pixels in the x-direction, because the image is the same everywhere in that direction.



Here a sine function with a higher frequency is used to generate the image, so the two dots are further away from the origin to represent the higher frequency. Remember the scale property of the Fourier Transform? Here it's illustrated very well: the image contracts, and its spectrum becomes wider.



In the next image, the sine function doesn't tile: if you'd put the same image twice on top of each other, you wouldn't see a sine anymore in the y-direction (while in the previous two examples you would). This isn't considered a real sine anymore by the spectrum either, and it doesn't contain just two dots, but a line.



One of the properties of the 2D FT is that if you rotate the image, the spectrum will rotate in the same direction:



The following image shows the sum of 2 sine functions, each in another direction (Plasma effects are often made this way):



The following image shows how lines in an image often generate perpendicular lines in the spectrum:



The sloped lines in the spectrum here are obviously due to the sharp transition from the sky to the mountain.



The FT of a rectangular function is a 2D sinc function:



And here's the FT of a tillable texture, since it's tillable there are no abrupt changes on the horizontal and vertical sides, so there are no horizontal and vertical lines in the spectrum:



2D Filters

Now comes the most interesting application of the FT on images: you can easily apply all sorts of filters to the spectrum, again by multiplying them with a 2D transfer function, or by making some parts of the spectrum zero, or just applying some whacko formula to the spectrum. After doing that, take the inverse FT of the modified spectrum to get the filtered image.

Here's part of the code for a program that'll allow you to select different images (a PNG, modified versions of it, and some generated functions), and then after pressing space, allows you to apply different filters and see their effect. The full code can be downloaded here: fourier2d.cpp.

This code doesn't contain much new, it's much more interesting to run it and study the results of the filters.

Once again, first come all the declarations of functions and variables. f2 and F2 will become the buffers for the filtered versions of the original image and spectrum.

// working with fixed sizes for simplicity in this tutorial
const int W = 128; //the width of the image
const int H = 128; //the height of the image

double fRe[H][W][3], fIm[H][W][3], fAmp[H][W][3]; //the signal's real part, imaginary part, and amplitude
double FRe[H][W][3], FIm[H][W][3], FAmp[H][W][3]; //the FT's real part, imaginary part and amplitude
double fRe2[H][W][3], fIm2[H][W][3], fAmp2[H][W][3]; //will become the signal again after IDFT of the spectrum
double FRe2[H][W][3], FIm2[H][W][3], FAmp2[H][W][3]; //filtered spectrum

double pi = 3.1415926535897932384626433832795;

void draw(int xpos, int yPos, int w, int h, const double *g, bool shift, bool neg128);
void DFT2D(int w, int h, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm);
void FFT2D(int w, int h, bool inverse, const double *gRe, const double *gIm, double *GRe, double *GIm);
void calculateAmp(int w, int h, double *ga, const double *gRe, const double *gIm);

The main function loads a PNG image first, and will then start the first loop, the loop that lets you try out different modified versions of the PNG image and some other generated signals:

int main(int /*argc*/, char */*argv*/[])
{
  screen(3 * W,4 * H + 8, 0,"2D FFT and Filters");
  std::vector img;
  unsigned long dummyw, dummyh;
  if(loadImage(img, dummyw, dummyh, "pics/test.png"))
  {
    print("image pics/test.png not found");
    redraw();
    sleep();
    cls();
  }
  //set signal to the image
  for(int y = 0; y < H; y++)
  for(int x = 0; x < W; x++)
  {
    fRe[y][x][0] = img[W * y + x].r;
    fRe[y][x][1] = img[W * y + x].g;
    fRe[y][x][2] = img[W * y + x].b;
  }

  int ytrans=8; //translate everything a bit down to put the text on top

  //set new FT buffers
  for(int y = 0; y < H; y++)
  for(int x = 0; x < W; x++)
  for(int c = 0; c < 3; c++)
  {
    FRe2[y][x][c] = FRe[y][x][c];
    FIm2[y][x][c] = FIm[y][x][c];
  }

  bool changed = 1, endloop = 0;
  while(!endloop)
  {
    if(done()) end();
    readKeys();

Here's a small part of the input part of the first loop, it looks pretty messy here, only a few keys are shown here, the code for all keys is included in the downloadable file.

    if(keyPressed(SDLK_z) || changed)
    {
      for(int y = 0; y < H; y++)
      for(int x = 0; x < W; x++)
      for(int c = 0; c < 3; c++)
      {
        fRe2[y][x][c] = fRe[y][x][c];
      } changed = 1;
    } //no effect
    if(keyPressed(SDLK_a))
    {
      for(int y = 0; y < H; y++)
      for(int x = 0; x < W; x++)
      for(int c = 0; c < 3; c++)
      {
        fRe2[y][x][c] = 255 - fRe[y][x][c];
      }
    changed = 1;} //negative
    if(keyPressed(SDLK_b))
    {
      for(int y = 0; y < H; y++)
      for(int x = 0; x < W; x++)
      for(int c = 0; c < 3; c++)
      {
        fRe2[y][x][c] = fRe[y][x][c]/2;
      }
      changed = 1;
    } //half amplitude


    //ETCETERA... *snip*

    if(keyPressed(SDLK_SPACE)) endloop = 1;

If a key was pressed, the new version of the image and its spectrum will be drawn. If the first loop was done (by pressing space), the second loop is initialized:

    if(changed)
    {
      //Draw the image and its FT
      calculateAmp(W, H, fAmp2[0][0], fRe2[0][0], fIm2[0][0]);
      draw(0, ytrans, W, H, fRe2[0][0], 0, 0);  draw(W, 0+ytrans, W, H, fIm2[0][0], 0, 0);  draw(2 * W, 0+ytrans, W, H, fAmp2[0][0], 0, 0); //draw real, imag and amplitude
      FFT2D(W, H, 0, fRe2[0][0], fIm2[0][0], FRe[0][0], FIm[0][0]);
      calculateAmp(W, H, FAmp[0][0], FRe[0][0], FIm[0][0]);
      draw(0,H + ytrans, W, H, FRe[0][0], 1, 1);  draw(W, H + ytrans, W, H, FIm[0][0], 1, 1);  draw(2 * W, H + ytrans, W, H, FAmp[0][0], 1, 0); //draw real, imag and amplitude
      print("Press a-z for effects and space to accept", 0, 0, RGB_White, 1, ColorRGB(128, 0, 0));
      redraw();
    }
    changed = 0;
  }
  changed = 1;
  while(!done())
  {
    readKeys();

Here's a small part of the input code to apply filters: a Low Pass, High Pass and Band Pass filter are given. The rest of the keys is in the downloadable file.

    if(keyPressed(SDLK_g))
    {
      for(int y = 0; y < H; y++)
      for(int x = 0; x < W; x++)
      for(int c = 0; c < 3; c++)
      {
        if(x * x + y * y < 64 || (W - x) * (W - x) + (H - y) * (H - y) < 64 || x * x + (H - y) * (H - y) < 64 || (W - x) * (W - x) + y * y < 64)
        {
          FRe2[y][x][c] = FRe[y][x][c];
          FIm2[y][x][c] = FIm[y][x][c];
        }
        else
        {
          FRe2[y][x][c] = 0;
          FIm2[y][x][c] = 0;
        }
      }
      changed = 1;
    } //LP filter

    if(keyPressed(SDLK_h))
    {
      for(int y = 0; y < H; y++)
      for(int x = 0; x < W; x++)
      for(int c = 0; c < 3; c++)
      {
        if(x * x + y * y > 16 && (W - x) * (W - x) + (H - y) * (H - y) > 16 && x * x + (H - y) * (H - y) > 16 && (W - x) * (W - x) + y * y > 16)
        {
          FRe2[y][x][c] = FRe[y][x][c];
          FIm2[y][x][c] = FIm[y][x][c];
        }
        else
        {
          FRe2[y][x][c] = 0;
          FIm2[y][x][c] = 0;
        }
      }
      changed = 1;
    } //HP filter

    if(keyPressed(SDLK_t))
    {
      for(int y = 0; y < H; y++)
      for(int x = 0; x < W; x++)
      for(int c = 0; c < 3; c++)
      {
        if((x * x + y * y < 256 || (W - x) * (W - x) + (H - y) * (H - y) < 256 || x * x + (H - y) * (H - y) < 256 || (W - x) * (W - x) + y * y < 256) && (x * x + y * y > 128 && (W - x) * (W - x) + (H - y) * (H - y) > 128 && x * x + (H - y) * (H - y) > 128 && (W - x) * (W - x) + y * y > 128))
        {
          FRe2[y][x][c] = FRe[y][x][c];
          FIm2[y][x][c] = FIm[y][x][c];
        }
        else
        {
          FRe2[y][x][c] = 0;
          FIm2[y][x][c] = 0;
        }
      }
      changed = 1;
    } //BP filter

    //ETCETERA... *snip*

This is the part of the second loop that draws the filtered spectrum and signal, and the final part of the main function:

    if(changed)
    {
      //after pressing a key: calculate the inverse!
      FFT2D(W, H, 1, FRe2[0][0], FIm2[0][0], fRe[0][0], fIm[0][0]);
      calculateAmp(W, H, fAmp[0][0], fRe[0][0], fIm[0][0]);
      draw(0, 3 * H + ytrans, W, H, fRe[0][0], 0, 0);  draw(W, 3 * H + ytrans, W, H, fIm[0][0], 0, 0);  draw(2 * W, 3 * H + ytrans, W, H, fAmp[0][0], 0, 0);
      calculateAmp(W, H, FAmp2[0][0], FRe2[0][0], FIm2[0][0]);
      draw(0, 2 * H + ytrans, W, H, FRe2[0][0], 1, 1);  draw(W, 2 * H + ytrans, W, H, FIm2[0][0], 1, 1);  draw(2 * W, 2 * H + ytrans, W, H, FAmp2[0][0], 1, 0);
      print("Press a-z for filters and arrows to change DC", 0, 0, RGB_White, 1, ColorRGB(128, 0, 0));
      redraw();
    }
    changed=0;
  }
  return 0;
}

The functions FFT2D, draw and calculateAmp are the same as before again and not shown here. They're also in the downloadable file.

Here's a possible output of the program:



The top row shows the original image, below that is its spectrum (the amplitude on the right), the third row shows the spectrum with a low pass filter applied to it: only the low frequency components remain. The bottom row shows the result of the Inverse FT on the new spectrum: all high frequency components of the image are removed, and the image becomes blurred.

Here's another example, which shows what happens if you set the imaginary part of the spectrum to 0. To get this, first press space and then press the b key in the program.



More on different types of filters follows in the next sections.

The DC Component

The center of the spectrum is the DC component of the picture, and represents the average color of the picture: if you calculate the IDFT of a spectrum with only the DC component left, you get a flat image with only one color: the average of the original image. In the program for which the code was given above, first accept the image by pressing space, and then you can add or remove the DC component by using the arrow keys, get the full spectrum again by pressing the a key (or the q key on azerty keyboards), and make the spectrum zero by pressing the m key (the , key on azerty keyboards). To get only the DC component, first press m to remove the spectrum, then the up arrow to get only the DC component back.

This is the original image (the bright blue line in the spectrum probably comes from the sharp edges from the cooling fin):



Here's the same image with the DC component removed (note the black dot in the center of the spectrum). You can't see the whole story in fact, all the parts of the image that look black are actually negative, since this picture represents the original image with the average color substracted from it. On the right is the amplitude of the image instead, which reveals the negative parts.

Image with its DC component removedThe amplitude of the image with its DC component removed

And here below only the DC component is left. Only a single dot remains in the spectrum. It looks white on the computer screen, but in reality it are 3 large floating point numbers that contain the DC color information. The DC component of an image's spectrum is usually very large, it contains the most "energy": as you could see on the previous image, removing this single dot from the spectrum makes the image a whole lot darker. Energy has to be understood in terms of Information here.

Only the DC component of the image remains

This is the average color of the image, you can call it the ultimate blur, what you'd see if you were standing very far away from the image, or what you'd get if you took the sum of the color of all pixels, and divided the result though the total number of pixels.

Low Pass Filters: Blurring

Low frequencies in an audio represent the bass of the music, but in pictures, it represents the blurriest parts and gradients. Sharp edges and lines have high frequencies.

An image can be blurred by, for each pixel, calculating the weighed average of that pixel and its neighbours, using a convolution matrix: that's the way Photoshop and Paint Shop Pro do it, for example, you can create such a convolution matrix with the "User Defined" filter in these programs. But, since the convolution in the spatial domain is the same as a multiplication in the frequency domain, we can also blur an image, by multiplying the spectrum with the transfer function of a low pass filter. The transfer function of a low pass filter makes all high frequency components zero or at least weakens them, while keeping or amplifying the low frequency ones.

For very blurry blurs, a very large convolution matrix is required, and this would require a lot of calculations. Taking the Fast Fourier Transform, then multiplying the spectrum, and then taking the Inverse FFT, goes much faster for heavy blurs. You can also create much nicers blurs easier and more intuitively by using the spectrum

The more high frequencies you remove of the spectrum, the blurrier the image, and the more calculations would be needed in the spatial domain:








In the above images, a circular section of the spectrum is left. A much nicer blur would be created by not using such a "sharp" circle, but a gaussian kernel, which exponentially decreases in value from the center. That would give a gaussian blur.

You can also, for example, keep a square one, but round ones should give nicer blurs:

Side note: for some types of blur, such as gaussian blur, there are still other faster algorithms that don't require the FFT nor a large kernel, in the case of gaussian blur you can approximate it very well by doing three box blurs that take linear time for any size of box in a row, see the Filtering tutorial of this series for a bit more on that.

High Pass Filters

A high pass filter on an image keeps only the high frequency components. Since, by applying a high pass filter, the DC component of the spectrum is removed too, the resulting image can have negative pixel values that can't get drawn. To overcome this, the high pass filter of Photoshop adds 128 (half of the maximum value 255) to each color component the resulting pixels, so grey represents zero. Here, we'll look at the positive part of the image, the amplitude (revealing the negative values), and the image with the DC component added again instead.

A high pass filter is exactly the opposite of the low pass filters, so now a circular section in the center of the spectrum is removed. On the left is the resulting positive real part of the image, in the center the spectrum with the circle removed, and on the right the amplitude of the image:



To see much better what's going on, add the DC component to it again:



It can be seen that only the high frequency parts of the image are left: subtle gradients and color changes are gone, only the edges of objects and especially the cooling fin are still recognisable.

Photoshop, instead of adding the DC component, adds grey to the image to make all pixels positive, so the result of the High Pass filter in Photoshop is something like this:



If we use a higher radius for the removed circle, only the very highest frequencies remain, only the cooling fin still looks pretty nice:



A high pass filter can also be done by first blurring the image, and then substracting the blurred image from the original.

After seeing those pictures you might wonder if there is actually something useful that can be done with a High Pass Filter? Well, it can for example be used to make better tillable textures, take for example this grass texture:



If you tile it, it looks like this:



It looks pretty ugly, because there are obvious bright and dark spots in the image, and these look very repetitive. These large areas of bright and darker color are very low frequency components, so they can be removed with a subtle High Pass Filter!

Let's process the image to our program, apply a High Pass filter with a very small radius to it, and bring the DC component back: the DC component is the lowest frequency of all, just a flat color, so it can't look repetitive, and is very important because it contains the green color of the grass. As you can see on the third row on the right in the screenshot, a very small circular section of the spectrum is removed, and in the centre of the circle is a single white point which is the DC component.



At the bottom row a new version of the grass texture appeared, that looks already much better when tiled if you take a certain distance from it:



You can still recognise where the sides are, because the source image actually wasn't a perfectly tillable one. If the source image would've been perfectly tillable, the result would've been so as well. On a beautiful photorealistic texture of a rocky wall, with however a large dark spot in it that makes the rocky wall repetitive when tiled, the result of this high pass filter would've been very useful.

The source code of the program was a little bit modified to get a high pass filter with a smaller radius under the "SDLK_j" button.

Side note: For sharpening, too, there are even faster algorithms than with FFT, such as using fast blur and then computing the following sum of images: original + (original - blur) * amount. This is "unsharp masking"

Band Pass Filters

Band Pass filters leave though only frequencies that are between a certain lowest and a highest frequency. Your radio uses the 1D version of this to listen to a station with a certain frequency. Again the DC component is removed by such a filter, so we add it again, because without it the image is too dark to see it. Here's the original image again, and an example of such a BP filter with DC component:





The sum of many images like this one together (but with the DC component added only once of course) forms the original image again. Here's are a few more BP filters, that leave through higher frequencies:







And here's the result of a much thinner BP filter, the thinner the BP filter, the more it can be seen how the image is a sum of sine functions:



Note: not all bandpass examples are included in the program by default, but you can easily get them by changing numbers of the BP filters in the code (under SDLK_r and SDLK_s in the second input loop).

Keeping it Real

Up to this point, we always calculated the FT of each channel separately, and left the imaginary part black. This is a big loss of resources, since there are 3 unused imaginary channels.

Since the result of the FT of a real function is symmetrical in the complex domain, half the information is in fact redundant. So it's possible to store the result of the FT into one real array anyway: Place the DC component in the center, on one side put one half of the real part, on the other side one half of the imaginary part. For even sized input, there will also be one value that is zero in the imaginary part and has some non-zero value in the real part. That one value can go in the remaining index. This transform is perfectly reversible, but it requires taking care of indices correctly. Providing the code here is currently beyond the scope of this already long tutorial.

Another way to avoid complex numbers is to use a real transform, such as the DCT (Discrete Cosine Transform). Several similar such transforms exist, and have similar "Fast" variants, but that too is beyond the scope here for now.

Copyright (c) 2004-2018 by Lode Vandevenne. All rights reserved.